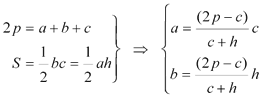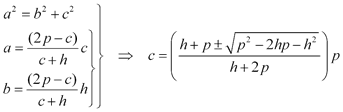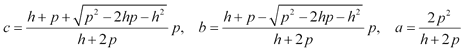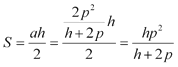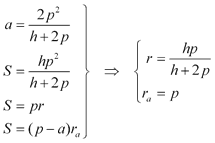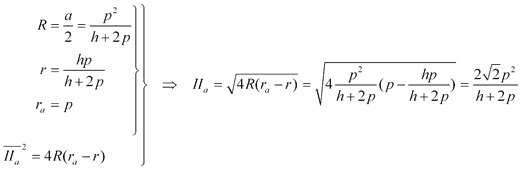De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 466.

En un triángulo rectángulo se conocen el perímetro 2 p y la altura h correspondiente al ángulo recto y se pide obtener en función de p y h :

1. Los tres lados del triángulo y su área.
2. Condición para que el problema sea posible.
3. Los radios del círculo inscrito y del círculo ex - inscrito correspondiente al ángulo recto.
4. La distancia entre los centros de ambos círculos.
5. Construcción geométrica del triángulo dados p y h.(Para ello conviene usar el círculo ex - inscrito indicado)

Matemática Elemental (1933), Tomo II, N .1, Enero, propuesto en la ETSI de Caminos (1931) p .14, N.39.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de mayo de 2008)

APARTADO (1)

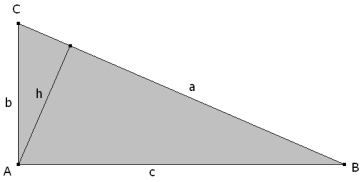
Suponemos que b y c son los catetos y que a es la hipotenusa. En estas condiciones podemos expresar el perímetro 2p en función de los lados y el área S de dos modos distintos en función de los lados y la altura.

De las expresiones anteriores podemos despejar la hipotenusa y un cateto.

Imponemos ahora la condición de triángulo rectángulo mediante el teorema de Pitágoras.

donde introduciendo los resultados anteriores para la hipotenusa y un cateto, obtenemos para c las dos expresiones para los catetos. Si fijamos de acuerdo con el dibujo el mayor valor para el cateto c nos queda

Su área se expresará como

APARTADO (2)

Como hemos impuesto las condiciones del enunciado, para que existan los catetos y por tanto el triángulo bastará que la expresión dentro de la raíz cuadrada sea positiva

APARTADO (3)

Como sabemos expresar el área del triángulo en función del radio inscrito o del ex-inscrito tenemos

APARTADO (4)

Recordemos de distintos problemas de esta revista que

donde R es el radio del círculo circunscrito que en un triángulo rectángulo es la mitad de la hipotenusa y obtenemos

APARTADO (5)

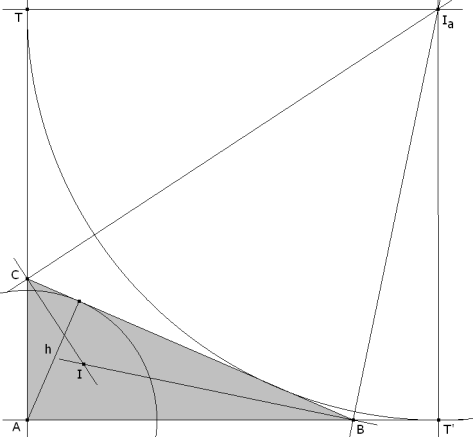
Basta observar la figura y recordar que la distancia del vértice A al punto de contacto T es p al igual que el radio del círculo ex-inscrito opuesto a A, para ver que el cuadrilátero ATI_aT’ es un cuadrado; por tanto, podemos deducir un método de construcción.

1. trazamos un cuadrado de lado p
2. por uno de los vértices de dicho cuadrado, que llamamos A, trazamos un círculo de radio h
3. por el vértice opuesto a A, que llamamos I_a, trazamos un círculo de radio p
4. la tangente interna común a los dos círculos contiene a la base del triángulo
5. la intersección de la tangente anterior con los lados del cuadrado nos proporciona los otros dos vértices del triángulo que llamamos B y C
6. ABC es el triángulo buscado

Siguiendo estos pasos obtenemos la construcción dinámica que sigue

mueva los puntos azules

mueva los puntos azules