Problema 466.

En un triangle rectangle es coneixen el perímetre 2p i l’altura h corresponent a l’angle recte i es demana obtenir en funció de pi h:

a) Els tres costats del triangle i la seua àrea.

b) Condició per a què el problema siga possible.

c) Els radis del cercle inscrit i exinscrit corresponent a l’angle recte.

d) La distància entre els centres d’ambdós cercles.

e) Construcció geomètrica del triangle donats p i h. (Utilitzeu el cercle exinscrit indicat).

Solució de Ricard Peiró i Estruch:

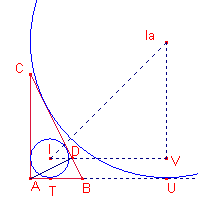
Siga el triangle rectangle , . Suposem .

Siga altura del triangle.

Siga T el punt de tangència de la circumferència inscrita i el costat .

Siga U el punt de tangència de la circumferència inscrita i el costat .

Siga I l’incentre i l’exincentre corresponent a l’angle recte.

Siga r el radi de la circumferència inscrita i el radi de la circumferència exinscrita corresponent a l’angle recte.

Sabem que per ser el triangle rectangle: , .

a)

L’àrea del triangle rectangle és: .

.

Aleshores, (1)

(2)

. Aplicant el teorema de Pitàgores i l’expressió (2):

.

Aplicant l’expressió (1):

. Aleshores:

(3)

Anàlogament:

(4)

Resolent el sistema format per les expressions (3), (4).

,

.

L’àrea és:

.

b)

El problema té solució si .

Resolent la inequació, . La igualtat s’assoleix quan el triangle rectangle és isòsceles.

c)

, .

d)

Considerem la recta perpendicular al costat que passa per I, i la recta perpendicular al costat que passa per .. Ambdues rectes s’intersecten en el punt V.

Considerem el triangle rectangle i isòsceles .

.

Aplicant el teorema de Pitàgores al triangle :

.

e)

Mètode 1:

De l’apartat c) .

Dibuixar el segment

Dibuixar el segment perpendicular al segment .

Dibuixar la circumferència de centre que passa per U.

Dibuixar la circumferència de centre A i radi h.

Dibuixar la recta tangent m a les dues circumferències.

Aquesta recta talla el segment en el punt B.

Dibuixar la recta n perpendicular al segment en el punt A.

La intersecció de les rectes m i n és el punt C.

Dibuixar el triangle rectangle .

Amb Cabri:

Figura barroso466.fig

Applet created on 16/05/08 by User with CabriJava

Mètode 2:

De l’apartat a) , aleshores, .

a és quarta proporcional de .

Dibuixar el segment .

Dibuixar la circumferència de diàmetre .

Dibuixar la recta paral·lela al costat , a una distància h.

La recta talla la circumferència en el punt A.

Dibuixar el triangle rectangle .