Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 466
En un triángulo rectángulo se conocen el perímetro 2p y la altura h correspondiente al ángulo recto y se pide obtener en función de p y h :1) Los tres lados del triángulo y su área.2) Condición para que el problema sea posible.3) Los radios del círculo inscrito y del círculo ex-inscrito correspondiente al ángulo recto.4) La distancia entre los centros de ambos círculos.5) Construcción geométrica del triángulo dados p y h. (Para ello conviene usar el círculo ex-inscrito indicado)
Matemática Elemental (1933), Tomo II, N.1, Enero, propuesto en la ETSI de Caminos(1931) p.14, N. 39 .
Solución de Ricard Peiró i Estruch:
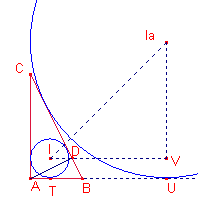
Sea el triángulo rectángulo 
, 
. Supongamos 
.
Sea 
altura del triángulo.
Sea T el punto de tangencia de la circunferencia
inscrita y el lado 
.
Sea U el punto de tangencia de la circunferencia
inscrita y el lado .
Sea I el incentro y 
el exincentro
correspondiente al ángulo recto.
Sea r el radio de la circunferencia inscrita y 
el radio de la circunferencia
exinscrita correspondiente al ángulo recto.
Sabemos que por ser el triángulo rectángulo: 
, 
.
a)
El área del triángulo rectángulo es: 
.
.
Entonces, 
(1)
(2)
. Aplicando el teorema de Pitágoras y la expresión (2):
.
Aplicando la expresión (1):
. Entonces:
(3)
Análogamente:
(4)
Resolviendo el sistema formado por las expresiones
(3), (4).
,
.
El área es:
.
b)
El problema tiene solución si 
.
Resolviendo la inecuación, 
. La igualdad se alcanza cuando el triángulo rectángulo
es isósceles.
c)
, .
d)
Consideremos la recta perpendicular al lado 
que pasa por I, y la
recta perpendicular al lado que pasa por .. Ambas rectas se intersectan en el punto V.
Consideremos el triángulo rectángulo y isósceles 
.
.
Aplicando el teorema de Pitágoras al triángulo :
.
e)
Método 1:
Del apartado c) .
Dibujar el segmento 
Dibujar el segmento 
perpendicular al
segmento 
.
Dibujar la circunferencia de centro que pasa por U.
Dibujar la circunferencia de centro A y radio h.
Dibujar la recta tangente m a las dos circunferencias.
Esta recta corta el segmento en el punto B.
Dibujar la recta n perpendicular al segmento en el punto A.
La intersección de las rectas m y n es el punto C.
Dibujar el triángulo rectángulo .
Amb Cabri:
Figura barroso466.fig
Applet created on 16/05/08 by
User with CabriJava
Método 2:
Del apartado a)
, entonces, 
.
a es cuarta
proporcional de 
.
Dibujar el segmento 
.
Dibujar la circunferencia de diámetro .
Dibujar la recta paralela al lado , a una distancia h.
La recta corta la circunferencia en el punto A.
Dibujar el triángulo rectángulo .