Problema 466.- (Propuesto por J. B. Romero Márquez, profesor
colaborador de
En un
triángulo rectángulo se conocen su perímetro 2p y la altura h
correspondiente al ángulo recto y se pide obtener en función de p y h:
(a) Los tres lados del triángulo
y su área
(b) Condición para que el problema
sea posible
(c) Los radios del círculo
inscrito y del excrito correspondiente al ángulo
recto
(d) La distancia entre los
centros de ambos círculos
(e) Construcción geométrica del
triángulo dados p y h. (Para ello conviene usar el círculo excrito indicado)
Matemática elemental (1993).
Tomo II, N.1. Enero. Propuesto en
Resolución: (Vicente Vicario García, I.E.S.
El Sur, Huelva)
Sea el triángulo rectángulo ABC con ángulo recto en el vértice A. Usaremos la notación habitual en la geometría del triángulo.
(a) En virtud del teorema de Pitágoras, e igualando las expresiones para el área del triángulo en función de los catetos b y c y en función de la hipotenusa a y la altura h sobre la misma, tenemos que
A partir de esta relación y de la condición del perímetro, tenemos entonces las siguientes relaciones que ligan los catetos b y c:
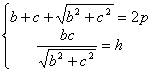[1]
De la primera de estas relaciones, y operando algebraicamente se tiene que
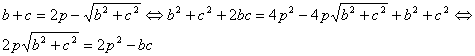
y sustituyendo la segunda relación de [1] en la última expresión
[2]
Podemos plantear ahora que
[3]
y en consecuencia b y c son las raíces de la ecuación de segundo grado
[4]
Entonces,
la hipotenusa viene dada por 
, y el área del triángulo por
.
(b) Estudiemos ahora la condición para que el problema sea posible. De la relación [4] observamos que es condición necesaria y suficiente para que tenga sentido el problema planteado que el discriminante de la ecuación cuadrática sea no nulo. Por tanto
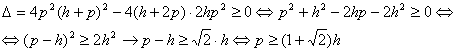
que es la condición buscada.
(c) Determinemos los radios del círculo inscrito y del excrito correspondiente al ángulo recto. Para el radio inscrito tenemos fácilmente que
y para el radio excrito 
, correspondiente al ángulo recto, teniendo en cuenta la
expresión clásica para el mismo, tenemos que
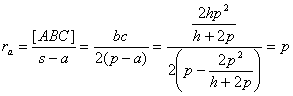
(d) Determinemos la
distancia entre los centros de ambos círculos. Esta distancia la denotaremos
como 
, donde I es el incentro del triángulo ABC
e 
es el centro del
círculo excrito al mismo y correspondiente al ángulo
recto.
Es bien conocido (por propiedades
del triángulo órtico) que el incentro
I del triángulo ABC es también el ortocentro de su
triángulo excentral 
(con vértices en los excentros). Sea d
la distancia entre el incentro I y el circuncentro O del triángulo ABC. Sea 
el circuncentro
del triángulo excentral. Tenemos entonces que O
es el punto medio del segmento 
ya que el circuncentro O
del triángulo ABC es también el
centro de la circunferencia de los nueve puntos del triángulo excentral.
Considerando
ahora el triángulo 
y aplicando la
expresión clásica para la longitud de la mediana 
en función de los lados 
, 
, (teorema de Apolunio),
tenemos que
Teniendo
en cuenta las relaciones clásicas de Euler 
y 
para los radios
inscrito, circunscrito y excrito, junto con la
relación 
(circunradio
del triángulo excentral), sustituyendo en la relación anterior, tenemos
que
de donde, finalmente, se tiene que
. [5]
Para determinar en función de p y h,
basta con observar que al ser ABC un
triángulo rectángulo, entonces 
, y sustituyendo en [5] los valores anteriores
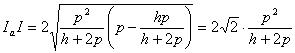
(e) Proporcionemos una construcción geométrica del triángulo dados p y h. Una construcción geométrica sencilla consiste en observar que
con 
magnitud que es fácil construir con regla y compás ya que el cociente de magnitudes constructibles también lo es. Entonces, es suficiente trazar una semicircunferencia de radio R (constructible) y trazar una paralela a distancia h de la misma (constructible). Los dos puntos de corte (simétricos) nos dan las posiciones del vértice A del ángulo recto buscado.