Problema 467.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva)

Sea un triángulo ABC. Consideremos los volúmenes de revolución , , obtenidos al hacer girar el triángulo alrededor de sus lados a, b, c respectivamente. Si , demostrar o refutar si , donde es el volumen de la esfera cuyo radio es el mismo que el de la circunferencia circunscrita al triángulo ABC.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva).

Utilizaremos la notación habitual en la geometría del triángulo. Necesitamos cuatro lemas para aplicarlos posteriormente a la resolución del problema.

Lema 1: “En todo triángulo ABC se cumple ”.

Demostración:

.

donde hemos empleado la fórmula de Herón y la fórmula para el área del triángulo, además de la conocida relación .■

Lema 2: “En todo triángulo se cumplen las desigualdades ”.

Demostración: Es claro que siendo , , y aplicando la desigualdad entre las media aritmética y geométrica tenemos que

[1]

Por otra parte, a partir de la fórmula de Herón del área de un triángulo y la relación clásica , tenemos

[2]

Entonces, llevando la expresión [2] a la [1], tenemos la primera desigualdad

dándose la igualdad si y sólo si el triángulo es equilátero. Para demostrar la segunda desigualdad, podemos aplicar el teorema de los senos generalizado y la desigualdad de Jensen a la función cóncava en el intervalo resultando

que es equivalente a la segunda desigualdad. De nuevo, la igualdad se da si y sólo si el triángulo es equilátero. ■

Lema 3: “En todo triángulo ABC se cumple ”.

Demostración: A partir de la conocida igualdad y la desigualdad entre las medias aritmética y geométrica tenemos que:

■

Lema 4: “En todo triángulo se cumple la desigualdad ”.

Demostración: Aplicando el lema 1 anterior y la expresión clásica tenemos

pero esta desigualdad es cierta ya que aplicando los lemas 2, 3 tenemos que

que es equivalente a la propuesta. ■

Centrándonos en nuestro problema, aplicando relaciones elementales relativas al baricentro y el teorema de Guldin sobre volúmenes de revolución, tenemos que

y utilizando las relaciones , y los lemas 2 y 4, obtenemos que

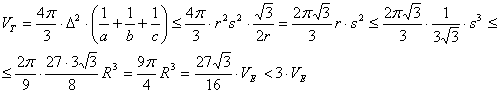
así que la proposición es cierta y se puede rebajar la constante 3 de la desigualdad por la constante