Problema 468

Para el aula.

Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (Valencia)

Sea ABC un triángulo de área S. Consideremos los puntos M, N sobre el lado BC, tal que CN=NM=MB . Sea M’ el punto simétrico de M respecto de A y N’ el punto simétrico de N respecto de A. Calcular el área del cuadrilátero BCM’N’.

Resolución

Grafiquemos de acuerdo al problema

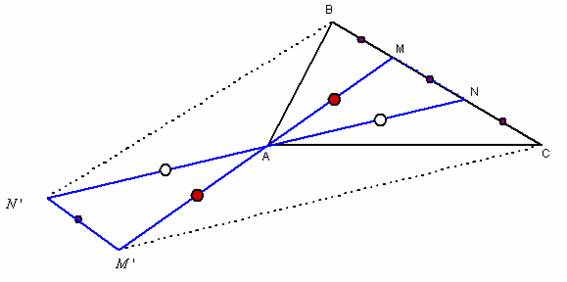
Como podemos observar el gráfico, nos damos cuenta que: M’N’ = MN = BM = NC

y N’A = AN, M’A = AM y caso (L.L.L.)

Además sabemos propiedad que: Si tenemos un triángulo y trazamos una mediana relativa a uno de sus lados, la mediana corta a dicho lado en dos segmentos iguales, generando dos triángulos de áreas iguales.

Entonces; y de los cuales concluimos que: o sea que:

Y por dato sabemos que: ; entonces

(Ver gráfico)

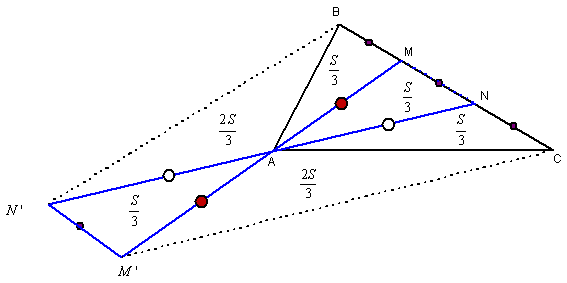
Aplicando la misma propiedad: también

y como ya es obvio el

Finalmente: