Problema 468
Sea ![]() un triángulo de área
S. Consideremos los puntos M, N sobre el lado
un triángulo de área
S. Consideremos los puntos M, N sobre el lado ![]() , tal que
, tal que ![]() . Sea M’ el punto simétrico de M respecto de A y N’ el punto
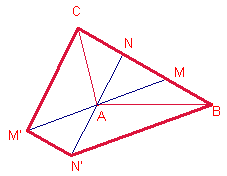
simétrico de N respecto de A. Calcular el área del cuadrilátero BCM’N’.
. Sea M’ el punto simétrico de M respecto de A y N’ el punto
simétrico de N respecto de A. Calcular el área del cuadrilátero BCM’N’.
 Solución
de Ricard Peiró:
Solución
de Ricard Peiró:
![]() , entonces,
, entonces, ![]() .
.
Dos triángulos que tienen la misma altura las áreas
son proporcionales a las bases.
Entonces: ![]() .
.
![]() . Análogamente,
. Análogamente, ![]() ,
, ![]() .
.
Los triángulos ![]() ,
, ![]() son simétricos respecto
del punto A, entonces:
son simétricos respecto
del punto A, entonces:
![]() .
.
Los triángulos ![]() ,
, ![]() tienen la misma altura
y las bases
tienen la misma altura
y las bases ![]() , entonces:
, entonces:
![]() .
.
Los triángulos ![]() ,
, ![]() tienen la misma altura
y las bases
tienen la misma altura
y las bases ![]() , entonces:
, entonces:
![]() . Entonces, el área del cuadrilátero BCM’N’ es:
. Entonces, el área del cuadrilátero BCM’N’ es:
![]() .
.
Con Cabri:
Figura barroso468.fig
Applet created on 2/06/08 by Ricard Peiró with CabriJava