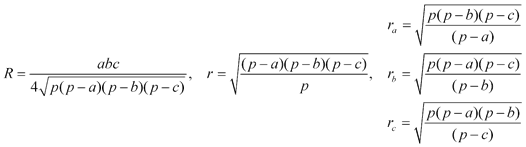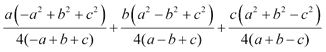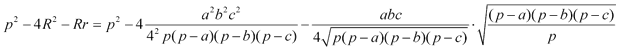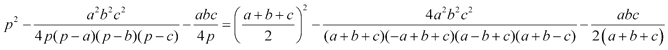Problema 469. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Demostrar la fórmula:

r_a Cos A+ r_bCos B+ r_c Cos C = 1/R ( p²- 4R²- Rr).

donde p, R, r, r_a, r_b, r_c, son el semiperímetro, radio del círculo circunscrito, radio del círculo inscrito, radios de los círculos exinscritos, al triángulo ABC, respectivamente.

Lemoine, E. (1900): El Progreso Matemático, (2), II, página 336

Lemoine, E. (1902): Revista Trimestral de Matemáticas Año II, Diciembre, N.8. página 192.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de junio de 2008)

Solución

A partir del punto 7.2 del extra nº 400 “Utiles simples para la resolución de problemas de triángulos” tenemos que

Ycomo por el teorema del coseno

El primer miembro de la ecuación queda

Introduciendo la expresión de R nos queda.

Y ahora que hemos eliminado las raíces sustiuyendo p en función de los lados, obtenemos en el interior del paréntesis

que queda como

Para el otro de la igualdad perseguida obtenemos

De donde cancelando las raíces y sustituyendo la expresión de p queda

que queda como

Por lo tanto los dos lados de la igualdad coinciden , coincidencia que pide el enunciado que probemos.