Problema 469.- (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid).

Demostrar la fórmula:

donde son el semiperímetro, radio de la circunferencia circunscrita, radio de la circunferencia inscrita y radios de las circunferencias excritas, al triángulo, respectivamente.

Lemoine, E. (1900). El progreso Matemático, (2), II, página 336.

Lemoine, E. (1902). Revista Trimestral de Matemáticas. Año II. Diciembre, N.8. página. 192.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo del problema, utilizaremos la notación habitual en la geometría del triángulo. Utilizaremos s para el semiperímetro del triángulo por ser más ampliamente reconocido que p. Emplearemos las bien conocidas expresiones clásicas siguientes para el área de un triángulo (entre ellas la fórmula de Herón), radios de las circunferencias excritas, relación entre los radios y los lados de un triángulo, y posteriormente, necesitaremos un lema que demostraremos.

, ,

Lema: “En todo triángulo ABC se cumple la relación: ”.

Demostración: Utilizaremos la fórmula de Herón y una de las relaciones anteriores

·

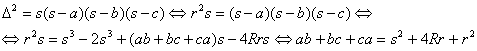Utilizando el teorema de los cosenos aplicado al triángulo ABC, podemos obtener la expresión siguiente

y en consecuencia, escribir la siguiente cadena de igualdades

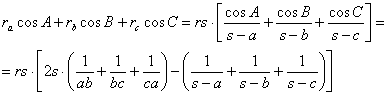
Finalmente, basta calcular los valores de los paréntesis del corchete anterior:

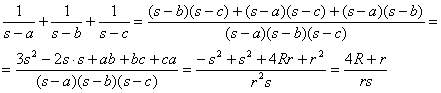
Y sustituyendo estas últimas expresiones tenemos que