Problema 470

De investigación

Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva

Dados los radios R_a, R _b, R _c de las circunferencias exinscritas al triángulo ABC, determinar las longitudes de los lados a, b ,c del mismo en función exclusivamente de los radios anteriores.

Vicario, V. (2008): Comunicación personal

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fenlabrada

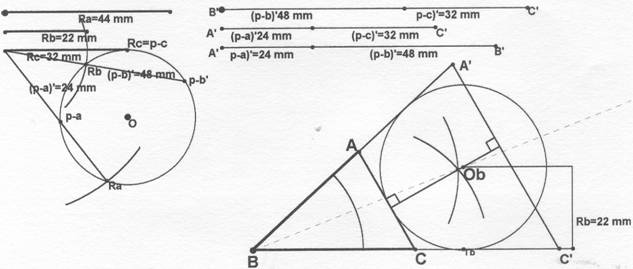
Se parte de la superficie S de un triángulo en función de los radios de las circunferencias circunscritas, del semiperimetro p y de los lados a, b y c: S = Ra(p-a) = Rb(p-b) = Rc(p-c) (1)

Se toma una superficie cualquiera S’ y se mantienes los factores Ra, Rb, R,c de cada igualdad.Se ha tomado la superficie S’ correspondiente a la superficie del triángulo de lados Ra, Rb y Rc para evitar la aplicación de potencia. Las alturas de este triángulo son (p-a)’ ( p-b)’ (p-c)’por lo tanto:

S’ = Ra(p-a)’ = Rb(p-b)’ = Rc(p-c)’ (2)

Dividiendo miembro a miembro (1) y (2) resulta:

(p-a)/(p-a)’ = (p-b)/( p-b)’ = (p-c)/(p-c)’

Los factores auxiliares (p-a)’ (p-b)’ (p-c)’ son proporcionales a los reales (p-a) (p-b) (p-c) por lo tanto el triangulo A’B’C’ será homotético al real ABC.

Para construir el triángulo auxiliar A’B’C’ hay que recordar que todo triángulo se cumple:

(p-b)’ + (p-c)’ = a’

(p-a)’ + (p-c)’ = b’

(p-a)’ + (p-b)’ = c’

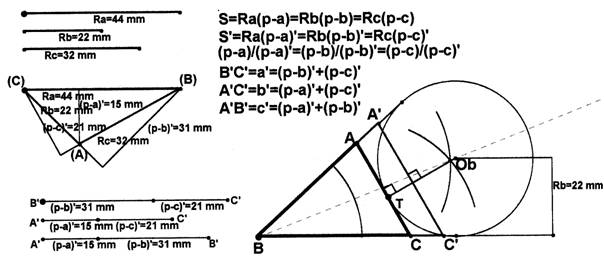
Las longitudes de los lados a, b, y c pedidos en el problema corresponden a los lados ABC del triángulo.

Cuando los tres exinradios pueden "formar" un triángulo, la construcción en relación al enunciado es válida, pero no lo es cuando no lo pueden construir.

2º método:

Aplicando la potencia que un punto P tiene con respecto a una circunferencia C, y, si al trazar arcos de centro P y de radio Ra, Rb, y Rc cortaran a la circunferencia C el problema se podrá resolver.

En la resolución por potencia se ha tomado la magnitud (p-c)’ = Rc.