Problema 470
Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva
Dados los radios ![]() ,
,![]() ,
,![]() de las circunferencias excritas al
triángulo ABC, determinar las
longitudes de los lados a, b ,c del
mismo en función exclusivamente de los radios anteriores.
de las circunferencias excritas al
triángulo ABC, determinar las
longitudes de los lados a, b ,c del
mismo en función exclusivamente de los radios anteriores.
----------------------------------------------------------------------------------------------------------
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)
Utilizaremos la
notación habitual en la geometría del triángulo y las relaciones clásicas para
el área de un triángulo ![]()
Necesitamos cuatro lemas que exponemos y demostramos a continuación.
Lema 1: “En todo triángulo ABC se cumple ![]() ”.
”.
Demostración:
![]()
![]()
![]() .
.
donde hemos empleado la fórmula de Herón ![]() y la fórmula
y la fórmula ![]() para el área del
triángulo, además de la conocida relación
para el área del
triángulo, además de la conocida relación ![]() .■
.■
Lema 2: “En todo triángulo se
cumple que ![]() ”.
”.
Demostración: Observemos que se cumple
![]() ■
■
Lema 3: “En todo triángulo se
cumple que![]() ”.
”.
Demostración: Veamos que ![]() ya que aplicando la
fórmula de Herón
ya que aplicando la
fórmula de Herón
![]() ■
■
Lema 4: “En todo triángulo se cumple que ![]() ”.
”.
Demostración: Basta con observar las relaciones
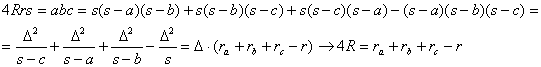 ■
■
Centrándonos en nuestro problema observamos que se tienen las relaciones
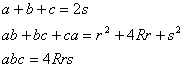 [1]
[1]
Por tanto, las longitudes de los lados a, b, c del triángulo ABC son las raíces reales de la siguiente ecuación cúbica
![]() [2]
[2]
Es conocido que tales
raíces se pueden expresar en función de radicales que involucran a sus
coeficientes. Finalmente, basta expresar r,
R y s como funciones exclusivas de ![]() . A tal efecto observemos que según los lemas 2, 3 y 4
tenemos
. A tal efecto observemos que según los lemas 2, 3 y 4
tenemos
![]() [3]
[3]
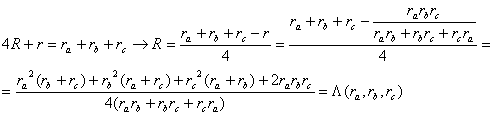 [4]
[4]
![]() [5]
[5]
Sustituyendo en la
ecuación [2] las expresiones ![]() ,
,![]() y
y ![]() de las relaciones [3],
[4], [5], obtenemos una ecuación algebraica cúbica cuyas raíces reales son las
longitudes de los lados del triángulo pedido y cuyos coeficientes están
expresados racionalmente como funciones exclusivas de los radios escritos
de las relaciones [3],
[4], [5], obtenemos una ecuación algebraica cúbica cuyas raíces reales son las
longitudes de los lados del triángulo pedido y cuyos coeficientes están
expresados racionalmente como funciones exclusivas de los radios escritos![]() .
.