|
Problema 471. De investigación. Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priegode Córdoba) Sean ABC un triángulo e I su incentro. Construir la cónica que pasa por A, B y C siendo tangente en B y C a las bisectrices BI y CI. Demostrar que esta cónica es siempre una hipérbola. Demostrar que la polar trilineal de cualquier punto P sobre ella pasa por el excentro correspondiente a A, y que si XYZ es el triángulo ceviano de P entonces Y, Z e I siempre están alineados. Polar trilineal. Sean ABC es un triángulo y P un punto de su plano. Si las rectas AX, BY, CZ cortan a los lados BC, CA, AB en los puntos X, Y, Z, es decir, si XYZ es el triángulo ceviano de P respecto de ABC, entonces, por el teorema de Desargues, los puntos de intersección X' = BC ∩ YZ, Y' = CA ∩ ZX, Z' = AB ∩ XY están alineados. La recta que los contiene se llama polar trilineal del punto P respecto del triángulo ABC. García, F.J. (2008) Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de junio de 2008) |
|
Solución |
|
|
Sea B* el haz de rectas que pasan por B y C* el haz de rectas que pasa por C. Por el teorema de Chasles-Steiner, sabemos que si definimos una homografía entre B* y C*, el lugar de la intersección de rectas homólogas en la homografía es una cónica. Las condiciones que explicita el profesor García Capitán en su enunciado nos ayudan a definir la homografía que define la cónica que se pide. Por ser un haz de rectas un espacio proyectivo de dimensión uno, tres pares de rectas homólogas determinan la homografía. h : B* ---> C*
Es claro que I es el polo de BC respecto a esta cónica; ya que es el punto de intersección de las tangentes por B y C. Por otra parte I es el centro de homografía y por lo tanto con él podemos obtener cualquier punto de la cónica. Si expresamos una recta cualquiera del haz B* com BY siendo Y un punto de la recta CA, como I es el centro de homografía la imagen de BY será CZ, siendo Z el punto donde YI corta al lado BA. Por lo tanto Z es la imagen de Y en la proyección de la recta CA sobre la recta BA con centro de proyección en I. Por lo tano, para construir un punto de la cónica haremos los siguiente:
Puede mover A, B, C, Y Puede mover A, B, C, Y
Hemos obtenido la cónica que pasa por A, B, C y es tangente a BI en B y a CI en C.
HEMOS PROBADO QUE COMO I ES EL CENTRO DE PROYECCIÓN ENTRE Y, Z; YZ SIEMPRE PASA POR I.
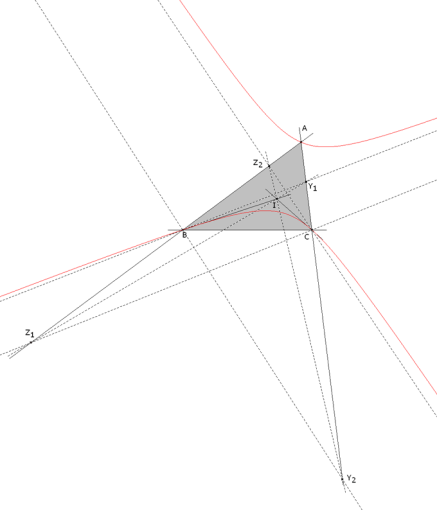
Como en la proyección de centro I del lado CA sobre el lado BA existen dos puntos (ver figura) Y1 y Y2 tales que BY1 es paralela a CZ1 y BY2 es paralela a CZ2, LA CÓNICA TIENE DOS PUNTOS EN EL INFINITO Y POR TANTO ES UNA HIPERBOLA.
Puede mover A, B, C, Y Puede mover A, B, C, Y
Sea X la intersección de AP con BC. Sea Y' la intersección de ZX con CA y sea Z' la intersección de XY con BA. Entonces Y' Z' es la polar trilineal de P. Pero por trazado Y' y Z' son homográficos en una homografía de la recta CA sobre la recta BA; pero la imagen de A en este caso coincide consigo misma lo que nos indica que al ser A la intersección de las rectas de la homografía, la homografía es una proyección. Hallemos el centro de proyección. Si Y coincide con A (está sobre la bisectriz de A), Y' coincide con Z' en A y AX' coincide con AI que es la bisectriz de A. Análogamente si Y está en B (sobre la bisectriz de B), X' y Z' coinciden en B y la polar es la bisectriz exterior de B. La bisectriz de A y la bisectriz exterior de B se encuentra en Ia que es el ex-incentro correspondiente al vértice A. POR LO TANTO IA ES EL CENTRO DE ESTA PROYECCIÓN Y EN CONSECUENCIA LAS RECTAS Y'Z' PASAN POR EL. Puede hacerse la comprobación colocando a Y en la bisectriz de C (sobre C), entonces la polar trilineal es la bisectriz externa de C que coincide con las anteriores en Ia. |