Problema 473. Para el aula. Propuesto por François Rideau, Maitre de Conférences à l'Université de Paris 7.

Dado un triángulo equilátero ABC, encontrar la transversal <PQR> con P sobre la recta BC, Q sobre la recta CA, y R sobre la recta AB tal que BP=CQ=AR.

Rideau, F. (2008): Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de junio de 2008)

Solución

PRESCINDIMOS DE LA CONDICION DEL PUNTO Q

Para atacar la solución prescindiremos inicialmente de la condición que obliga al punto Q.

figura 1

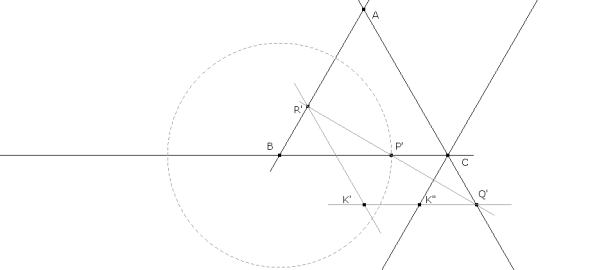
Trazamos una transversal que cumpla la condición AR’=BP’.

Sobre el lado AB tomamos un punto variable R’, y sobre BC tomamos un punto P’ tal que AR’=BP’ (compás).

Unimos R’ con P’ que corta a CA en Q’.

Una paralela por Q’ a BC corta a una paralela a CA por R’ en K’.

Esta misma paralela corta a una paralela a BA por C en el punto K”.

INTRODUCIMOS LA CONDICION DEL PUNTO Q

¡¡ Si el punto Q’ hallado fuera solución K’ coincidiría con K” !! Esto se traduce en que el punto K solución es la intersección entre el lugar geométrico del punto K’ y el lugar geométrico del punto K”.

El lugar geométrico de K” es la paralela a AB por el vértice C. El lugar geométrico de K’ es una cónica. Veamos:

figura 2

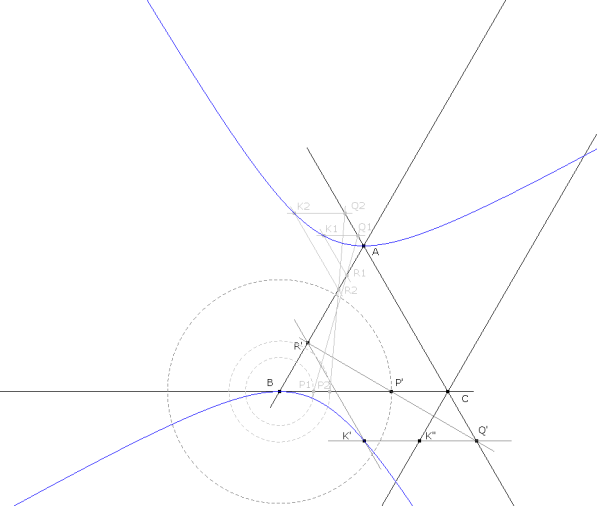
K’ es intersección de dos rectas paralelas respectivamente al lado BC y al lado CA. Es decir, pertenecen a los haces de rectas con vértices respectivos en el infinito del lado BC y del lado CA.

Para ver que entre Q’K’ y R’K’ existe una homografía basta ver que obtenemos Q’ a partir de R’ por medio de regla y compás. Es claro que la correspondencia h: AB→CA tal que h(R’)=Q’ es una biyección y por el principio de correspondencia anarmónica de Chasles, podemos asegurar que h es una homografía.

En consecuencia, al ser R’ y Q’ homográficos, tambien lo son las rectas R’K’ y Q’K’ y por tanto el lugar geométrico de K’ es una cónica.

Es claro que esta cónica además de pasar por el punto K’ pasa por A y B y dos puntos más K1 y K2 que trazamos por medio de dos puntos R1 y R2 sobre BA.

LA SOLUCION

El punto K solución está en las intersecciones de la cónica y la paralela al lado AB trazada por el vértice C.

La intersección recta y cónica puede obtenerse con regla y compás sin necesidad de trazar la cónica.

Como recta y cónica se encuentran en un máximo de dos puntos, hay hasta dos soluciones.

figura 3

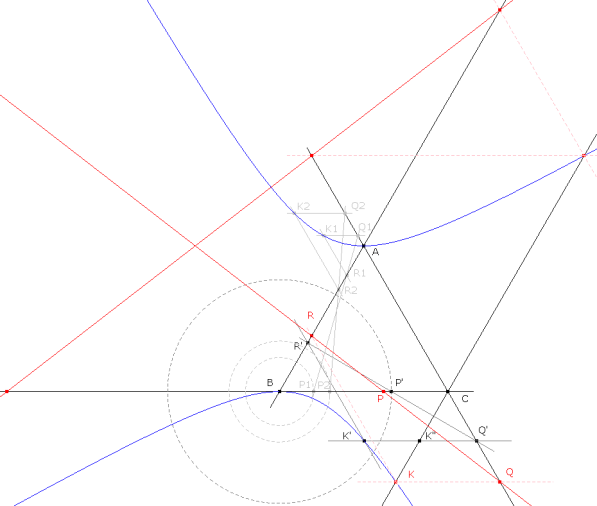
Por K, trazamos una paralela a CA que encuentra a AB en el punto R.

Por K, trazamos una paralela a BC que encuentra a CA en el punto Q.

La recta RQ corta a BC en el punto P.

RPQ es la transversal buscada.

Una segunda solución se obtiene de forma análoga con la segunda intersección.