Problema 473.- (Propuesto por Francois Rideau, Maitre de Conferences, Université de Paris 7).
Dado un triángulo equilátero ABC, encontrar la transversal <PQR> con P sobre la recta BC, Q sobre la recta CA, y R sobre la recta AB tal que se cumpla 
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)
Sin pérdida de generalidad
supondremos que el lado del triángulo equilátero vale la unidad. Sea x (
) la longitud común de los segmentos BP, CQ, AR. Entonces los segmentos BR y PC tienen como medida común
.. En virtud del teorema del Menelao
tenemos que
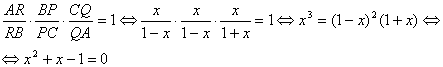
Finalmente, las soluciones de la ecuación cuadrática anterior son
, 
en la que, obviamente, sólo tiene sentido geométrico la primera solución 
, que proporciona la solución del problema.