Problema 475.  De investigación. Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva:  Sea ABC un triángulo. Probar o refutar si la condición necesaria y suficiente para que dicho triángulo sea equilátero, es que se anule el siguiente determinante:

donde h_am_a w_a son la altura, la mediana y la bisectriz interior que parten del vértice A del triángulo ABC, respectivamente. Análogamente se definen los demás términos del determinante respecto de los otros vértices. Vicario, V. (2008) Comunicación personal

Solución de  Profa. Mariela Lilibeth Herrera Ruiz

Cursante de la Maestría en Educación Matemática en la Universidad de Carabobo-Venezuela

Al decir que A es suficiente para B, estamos diciendo que A no puede ocurrir sin B, o cuando sea que ocurra A, B ocurrirá. Si A es una condición suficiente para B, entonces la relación lógica entre ellas es expresada como “Si A entonces B”, “B si A”, o “A ® B”.

En pocas palabras si el antecedente es verdadero, el consecuente tiene que ser verdadero, entonces: ¿será suficiente que un triángulo sea equilátero para que se anule el determinante planteado?, de hecho, sabemos que:

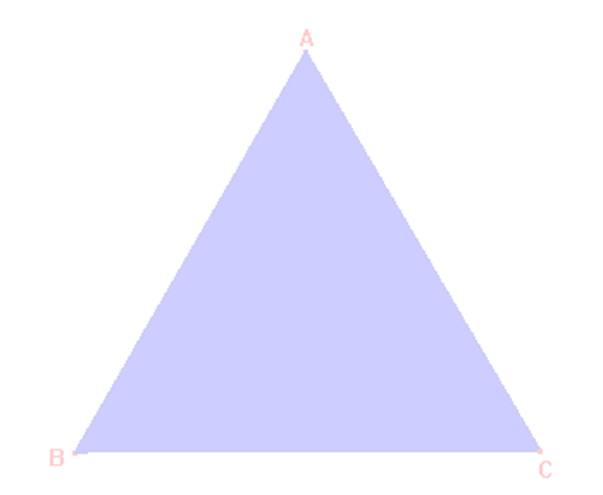Si ABC es un triángulo equilátero, entonces el determinante formado por  las alturas, medianas y bisectrices es nulo, ya que, la altura del triángulo equilátero es la misma  sin importar el vértice desde el que se este midiendo, por tanto, cualquiera de las tres alturas del triángulo nos genera el mismo valor, así, en la primera columna tendremos tres valores iguales, sin perdida de generalidades, sea a>0 la altura del triangulo equilátero, así el determinante buscado será:

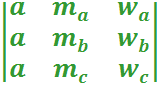
Ahora bien, si ABC es equilátero entonces la mediana, la bisectriz, la altura y la mediatriz son las mismas, así la matriz a la que se le calcula el determinante es una matriz de orden 3 cuyas entradas son idénticas será:  a³+a³+a³ - (a³+a³+a³)= 3a³ – 3a³=0

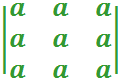
Por propiedades del determinante, sabemos que si dos columnas o filas de una matriz son idénticas el determinante es nulo, así, el determinante planteado es nulo, en conclusión, hemos probado que: El determinante formado por  las alturas, medianas y bisectrices de un triángulo equilátero es nulo

Sin embargo,  las condiciones necesarias  y suficientes consecuentemente están relacionadas: A es una condición necesaria para B solo en el caso de que B sea una condición suficiente para A. Debemos considerar que, una condición suficiente, por definición, es aquello que no puede ocurrir sin aquello para lo que es condición, en nuestro caso esto se traduce a decir que cada vez que el triángulo sea equilátero el determinante formado por  las alturas, medianas y bisectrices debe ser nulo.

En términos de la lógica A®B, implica que A es condición suficiente para B y B es condición necesaria para A, así, para que A sea verdadera se necesita que B lo sea, por ello se dice que B es condición necesaria para A. Así, es condición suficiente que el triángulo sea equilátero y es condición necesaria que el determinante formado por  las alturas, medianas y bisectrices de un triángulo sea nulo, sin embargo no es condición necesaria y suficiente  que el triángulo sea equilátero para que se anule el determinante planteado, de hecho se muestra un contraejemplo:

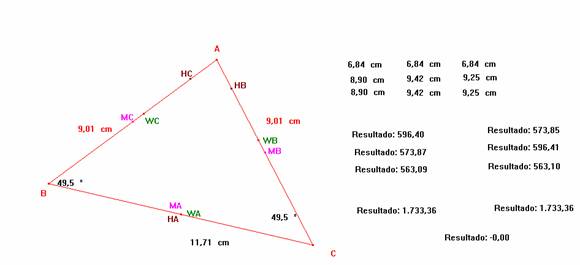
Cada vez que tenemos un triángulo isósceles, la altura, la bisectriz y la mediana (calculada desde el vértice opuesto a la base) pasan por el punto medio de la base, es decir, determinan el mismo segmento, por ende tienen la misma longitud, y al sustituir dichos valores en el determinante planteado tenemos una fila igual, además, la altura, la bisectriz y la mediana calculada desde un vértices de la base tienen la misma longitud si consideramos el otro vértice de la base, obtenemos un determinante de la forma:

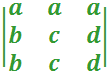
y como sabemos, por propiedades de los determinante si dos filas o dos columnas de un determinante son idénticos el determinante es nulo, cada vez que tengamos un triángulo isósceles (sin necesidad de que sea equilátero) tendremos que el determinante formado por las alturas, medianas y bisectrices será nulo.

Así hemos mostrado que no es condición necesaria y suficiente que un triángulo sea equilátero para que el determinante formado por sus alturas, medianas y bisectrices sea nulo.