Problema 475
Sea ![]() un triángulo. Probar o refutar si la condición
necesaria y suficiente para que dicho triángulo sea equilátero, es que
un triángulo. Probar o refutar si la condición
necesaria y suficiente para que dicho triángulo sea equilátero, es que 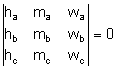
Solución de Ricard Peiró.
![]()
Si ![]() es equilátero,
es equilátero, ![]() ,
, ![]()
Entonces, el determinante tiene dos columnas linealmente dependientes, entonces,
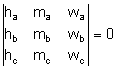 .
.
![]() Esta implicación no se
cumple siempre.
Esta implicación no se
cumple siempre.
Sea ![]() un triángulo isósceles,
un triángulo isósceles, ![]() .
.
En este caso ![]() ,
, ![]() ,
, ![]() .
.
Las filas 2ª y 3ª son proporcionales por tanto, 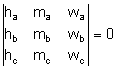 y el triángulo no es
equilátero.
y el triángulo no es
equilátero.