Problema 1.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva)
Sea ABC un triángulo. Probar o refutar si la condición necesaria y suficiente para que dicho triángulo sea equilátero, es que se anule el siguiente determinante:
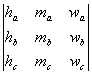
donde 
son la altura, la mediana y la bisectriz interior que parten
del vértice A del triángulo ABC, respectivamente. Análogamente se
definen los demás términos del determinante respecto de los otros vértices.
Utilizaremos la notación habitual en la geometría del triángulo. En la resolución del problema usaremos conocidas expresiones clásicas para el área del triángulo, longitud de las medianas y longitud de las bisectrices interiores.
[1]
, 
, 
[2]
, 
, 
[3]
Supondremos, sin pérdida de
generalidad que 
, lo que implica, según las relaciones [2] anteriores que 
. Sustituyendo tenemos que
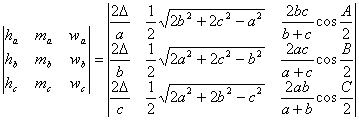
A partir de aquí utilizaremos la
notación abreviada 
, 
y 
. Entonces es claro que se tienen las relaciones 
. Extrayendo factores fuera del determinante y multiplicando
la primera fila por a, la segunda por b y la tercera por c (y dividiendo entonces el determinante
por abc), tenemos que
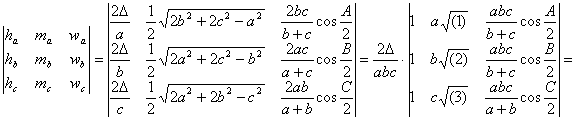
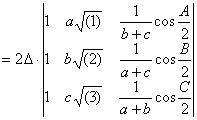
Desarrollando por los adjuntos de los elementos de la primera columna tenemos que el valor del determinante es
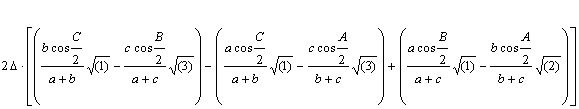
y reagrupando términos, tenemos que
Finalmente, basta observar que 
, 
, 
, y que 
y 
tienen signos
opuestos. Lo mismo ocurre con 
y 
, y con 
y 
. Entonces es claro que el determinante toma siempre valores
menores o iguales que cero. Si el determinante es nulo, entonces necesariamente
se cumple que 
y el triángulo es
equilátero. La condición suficiente es obvia ya que el determinante se anularía
por tener columnas iguales después de extracción de factores del mismo.