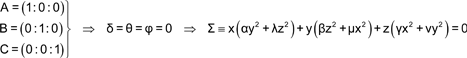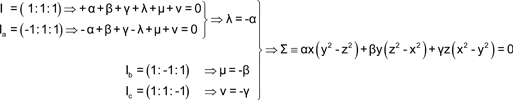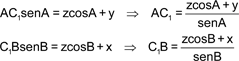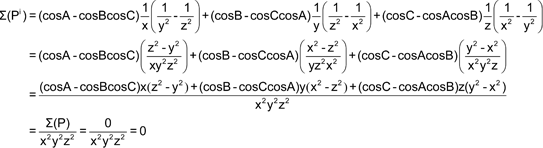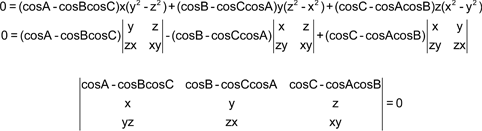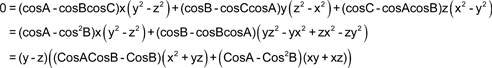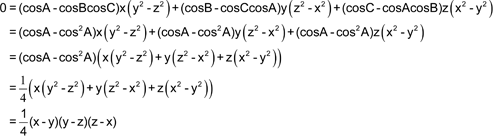Problema 476. De investigación. Propuesta de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona).

Dado un triángulo ABC y P un punto de su plano; llamamos A₁ a la proyección ortogonal de P sobre BC, B₁ a la proyección ortogonal de P sobre CA y C₁ a la proyección ortogonal de P sobre AB.

Sea Σ el lugar geométrico de los puntos P tales que las rectas AA₁, BB₁ y CC₁ son concurrentes; se pide:

1. Caracterizar el lugar Σ como una curva algebraica de orden n y determinar n.
2. Demostrar que el lugar Σ tiene al circuncentro O como centro de simetría.
3. Demostrar que los vértices del triángulo A, B, C, el incentro I, los ex-incentros I_a, I_b, I_c, el circuncentro O y el ortocentro H pertenecen al lugar Σ.
4. Hallar una ecuación del lugar Σ.
5. Demostrar que si P es un punto del lugar Σ,entonces Pⁱ el conjugado isogonal de P también es de la curva.
6. Demostrar que si P es un punto del lugar Σ, todas las rectas PPⁱ pasan por un punto fijo que se determinará.
7. ¿Cómo cambia el lugar Σ en el caso de que ABC sea un triángulo isósceles?

José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de julio de 2008)

Apartado 1

Caracterizar el lugar Σ como una curva algebraica de orden n y determinar n.

figura 1

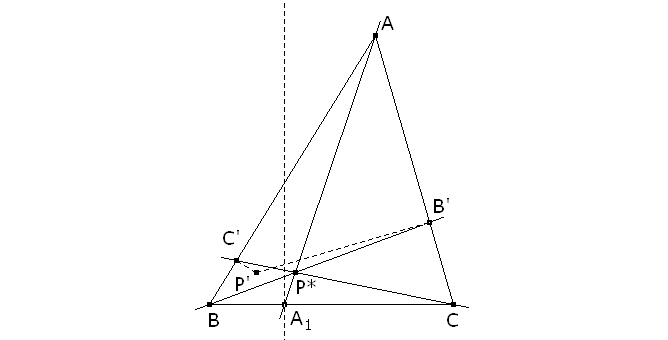
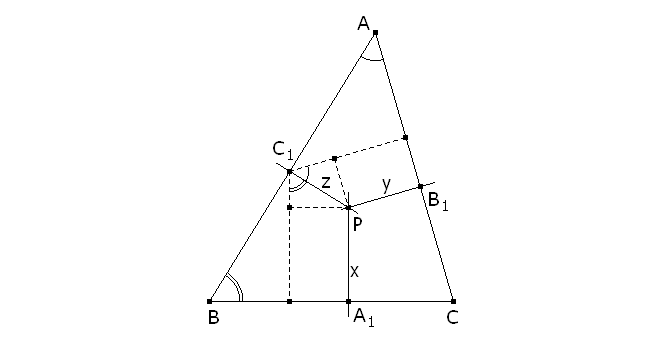
Para empezar tomaremos un punto P* sobre una ceviana cualquiera del triángulo. Por ejemplo la ceviana AA₁, al ser P* un punto cualquiera las otras dos cevianas serán BB’ y CC’. Si se cumplieran las condiciones del enunciado, la perpendiculat por B' al lado CA y la perpendicular por C' al lado AB se cortarían sobre la perpendicular por A₁ en el punto P; pero en general no será así, ya que B’ y C’ serían las proyecciones ortogonales respectivas, sobre CA y AB, de otro punto P’ (ver figura 1).

Para que P’ sea el punto P del lugar buscado, precisaríamos que este punto P’ estuviera además sobre la perpendicular a BC por el punto A₁. Es decir los puntos P del lugar Σ pedido son los puntos de intersección del lugar de los puntos P’, construidos como se indica en el párrafo anterior, y la perpendicular por A₁ al lado BC.

EL LUGAR DEL PUNTO P’ AL VARIAR P* SOBRE AA₁

figura 2

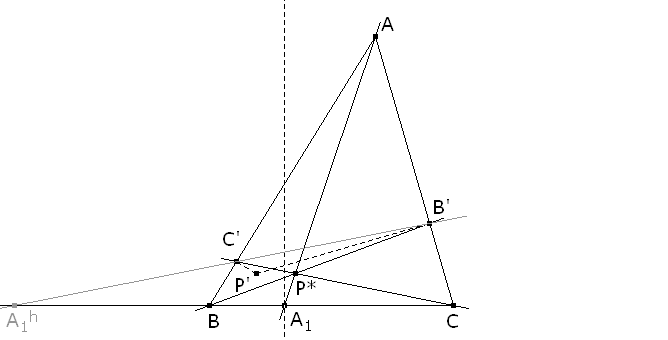
Veamos cual es el lugar geométrico de los puntos P’ al desplazarse P* a lo largo de la ceviana AA₁. La respuesta es sencilla. Dicho lugar, según el teorema de Chasles-Steiner, es una cónica. Como P* recorre una recta que pasa por A, la biyección BP*→CP* es una proyección del haz de rectas que pasan por B sobre el haz de rectas que pasan por C. Por tanto, la biyección B’→C’ es una proyección de la recta CA sobre la recta AB con centro (ver figura 2) en A₁^h. Si consideramos el cuadrilátero BCB’C’, vemos que A₁^h es el conjugado armónico de A₁ respecto B y C. La proyección, B’→C’, de CA sobre AB es, como tal, una homografía de la recta CA sobre la recta AB.

La perpendicular C’P’ al lado AB es una recta del haz de rectas que pasan por el punto del infinito de la dirección perpendicular a AB, análogamente B’P’ es una recta del haz de rectas que pasan por el punto del infinito de la dirección perpendicular a CA. Como B’ y C’ son homográficos, las recta B’P’ y C’P’ también son homográficas, y por el teorema de Chasles-Steiner el lugar de su punto de intersección (P’) es una cónica.

figura 3

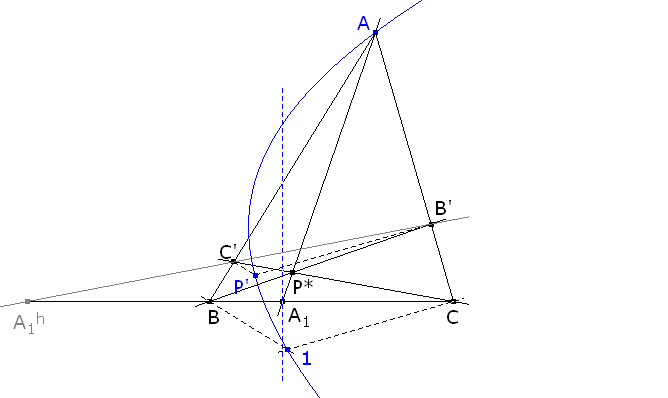
Esta cónica, por el mismo teorema de Chasles-Steiner, sabemos que pasa por los dos vértices de los haces de rectas que la generan, los puntos del infinito de las direcciones perpendiculares a los lados CA y AB; por la construcción sabemos que pasa también por el punto A y por el punto de intersección (1) de la perpendicular a AB en el punto B y la perpendicular a CA en el punto C. Estos cuatro puntos y el punto P’ construído, nos dan la cónica correspondiente a la ceviana AA₁ con la que podemos trabajar con regla y compás, sin necesidad de trazar la cónica.

Esta figura es dinámica en A, B, C, A₁ y P*

figura 4

La perpendicular a BC por A₁ corta a la cónica anterior, en general, en dos puntos P. El lugar de estos puntos P al variar A₁ sobre BC es el lugar pedido. Démonos cuenta de que podemos obtener la intersección de la recta perpendicular a BC por A₁ y de la cónica también con regla y compás.

EL LUGAR HALLADO ES UNA CURVA DE ORDEN 3

De los dos artículos de M. Chasles:

• Construcción de la curva de tercer orden determinada por nueve puntos (Comptes rendus, tomo xxxvi)
• Principio de correspondencia entre dos objetos variables ..., (Comptes rendus, tomo xli)

obtenemos el siguiente Teorema:

Dado un haz de cónicas K que pasan por cuatro puntos fijos y un haz de rectas R, si dichos haces se corresponden homográficamente, el lugar de los puntos P de intersección de una recta del haz R con su cónica correspondiente en el haz K es una curva de orden n=3.

La perpendicular por A₁ al lado BC es una recta del haz de rectas que pasan por el punto del infinito de la perpendicular al lado BC. Y la cónica (lugar de P’) es una cónica del haz de cónicas que pasan por el punto A, el punto 1, y los puntos del infinito de las perpendiculares respectivas a AB y CA.

La correspondencia entre la perpendicular por A₁ a BC y la cónica es una biyección y por el principio de correspondencia de Chasles, esa biyección es una homografía. Por lo tanto, de acuerdo con el teorema anterior

El lugar de los puntos P del enunciado es una curva de orden n=3.

En el apartado 4 veremos otra manera completamente distinta de llegar al mismo resultado.

Apartado 2

Demostrar que el lugar Σ tiene al circuncentro O como centro de simetría.

Sea P un punto del lugar Σ y sean A₁, B₁, C₁ sus proyecciones ortogonales sobre los lados BC, CA y AB respectivamente. Si las cevianas AA₁, BB₁ y CC₁ son concurrentes, por el teorema de Ceva tenemos

figura 5

Si P_o es el simétrico del punto P respecto al circuncentro O con proyecciones ortogonales sobre los lados A_o, B_o, C_o tenemos sobre los lados que

por lo que

y de acuerdo con el teorema de Ceva, las cevianas AA_o, BB_o y CC_o son concurrentes y por tanto, de acuerdo con el enunciado, P_o, el simétrico de un punto P de Σ respecto al circuncentro también pertenece a la curva Σ y en consecuencia

El circuncentro O es el centro de simetría de la curva Σ.

Como hemos visto que los puntos del infinito estaban en la dirección de las perpendiculares a los lados, la simetría respecto a O nos indica que las mediatrices a los lados son asíntotas de la curva.

Apartado 3

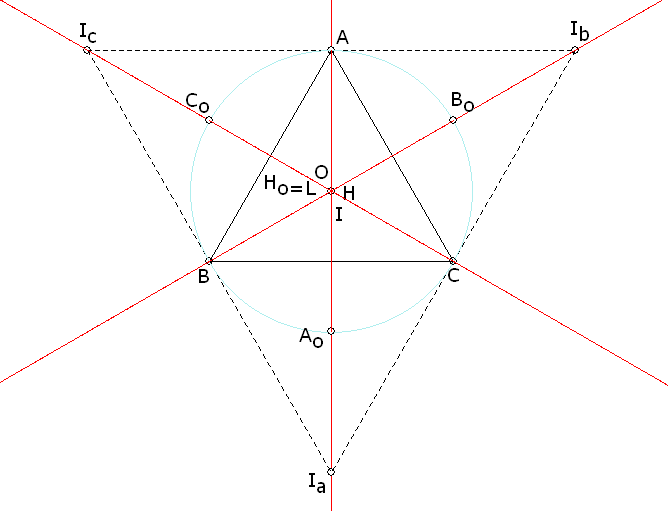
Demostrar que los vértices del triángulo A, B, C, el incentro I, los ex-incentros I_a, I_b, I_c, el circuncentro O y el ortocentro H pertenecen al lugar Σ.

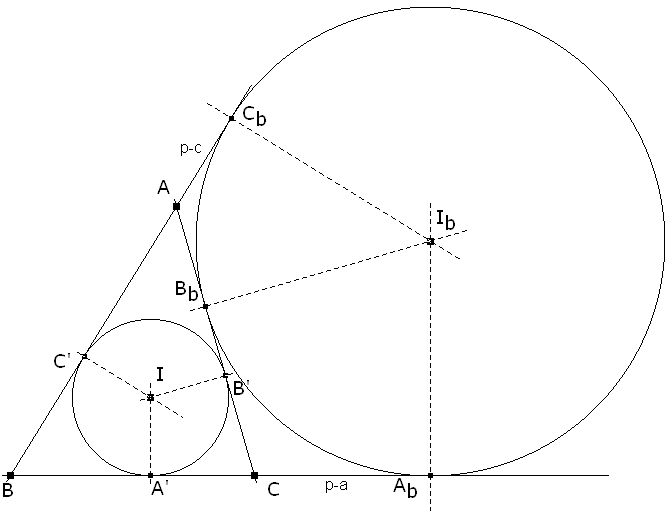
A, B, C

Basta darse cuenta de que los lados concurrentes en un vértice y la altura al lado opuesto son las tres cevianas que concurren en el propio vértice. Por tanto

Los vértices A, B, C pertenecen al lugar Σ.

El incentro I y los ex-incentros I_a, I_b, I_c

figura 6

Como I es el centro del círculo inscrito, sus proyecciones sobre los lados son los puntos de contacto de este círculo con el triángulo y por ello tenemos

entonces, por el teorema de Ceva las cevianas AA’, BB’ y CC’ son concurrentes y en consecuencia

El incentro I pertenece al lugar Σ.

En el caso de los ex-incentros podemos trabajar con I_b y extender el resultado a I_a e I_c. De nuevo, las proyecciones ortogonales sobre los lados son los puntos de contacto y por ello

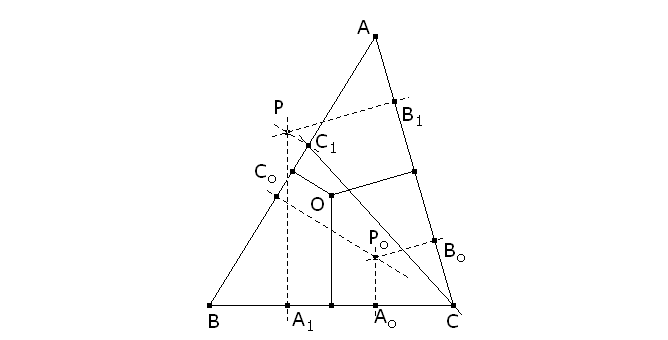
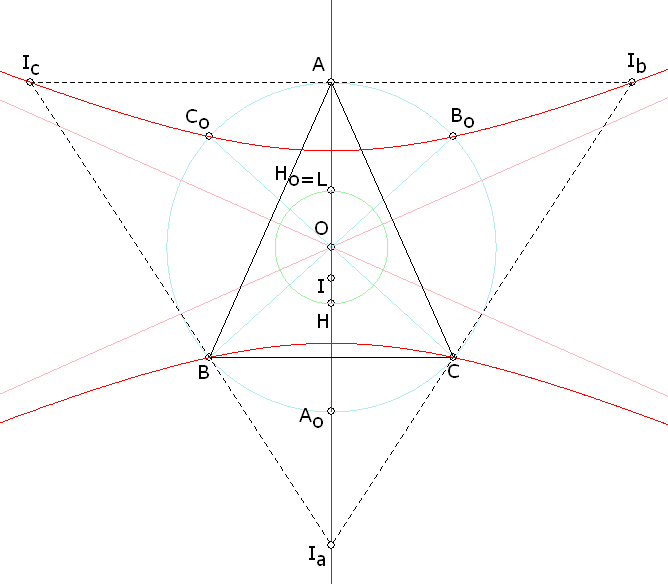
entonces, por el teorema de Ceva las cevianas AA_b, BB_b y CC_b son concurrentes, y en consecuencia

Los ex-incentros I_a, I_b, I_c pertenecen al lugar Σ.

El circuncentro O

Las proyecciones ortogonales sobre los lados del circuncentro son los puntos medios de los lados, por lo tanto las cevianas de esos puntos son las medianas que como sabemos concurren en el baricentro, en consecuencia

El circuncentro O pertenece al lugar Σ.

El ortocentro H

En este caso, las cevianas coinciden con las alturas que como sabemos son concurrentes en el propio ortocentro y en consecuencia

El ortocentro H pertenece al lugar Σ.

Esta figura es dinámica en A, B, C

figura 7

Vemos en la figura 7 la ubicación de los puntos anteriores sobre la curva y también la simetría con centro en O.

Apartado 4

Hallar una ecuación del lugar Σ.

Vamos a obtener la ecuación en coordenadas trilineales por dos métodos distintos.

METODO UNO

La ecuación general de una curva de tercer orden en coordenadas trilineales es de la forma

Como los vértices son de la curva

Como el incentro es de la curva y los ex-incentros también, nos queda

Como el ortocentro H pertenece a la curva y O es el centro de simetría, el simétrico de H respecto de O también es de la curva, Este simétrico recibe el nombre de punto de Longchamps L.

Como γ no es nulo, podemos escribir la ecuación como

METODO DOS

En este caso no realizaremos ninguna hipótesis sobre la ecuación. Impondremos, simplemente, la condición de concurrencia que exige el enunciado.

figura 8

Si tomamos como coordenadas trilineales del punto P las distancias a los lados del triángulo, podemos escribir

Análogamente

Expresando ahora la concurrencia de las cevianas AA₁, BB₁ y CC₁ mediante el teorema de Ceva.

Ecuación que ordenada queda como

Vemos que con este procedimiento, también podíamos haber respondido al primer apartado. Imponiendo la condición de concurrencia, obtenemos que la curva es de orden n=3.

Apartado 5

Demostrar que si P es un punto del lugar Σ,entonces Pⁱ el conjugado isogonal de P también es de la curva.

Sólo basta recordar que en coordenadas trilineales

y sustituyendo en Σ tenemos

Y en consecuencia

Si el punto P es del lugar Σ, también lo es su conjugado isogonal. Por eso se dice que Σ es isoconjugada (o invariante por conjugación isogonal).

Apartado 6

Demostrar que si P es un punto del lugar Σ, todas las rectas PPⁱ pasan por un punto fijo que se determinará.

Podemos reordenar la ecuación obtenida como un determinante y obtendremos la respuesta a esta cuestión

La nulidad del determinante expresa, en coordenadas trilineales, la condición de alineación de los tres puntos

y por lo tanto, como las coordenadas de L son fijas, podemos decir que

Si P es un punto del lugar Σ y su conjugado isogonal es Pⁱ, la recta PPⁱ pasa por un punto fijo L que es el simétrico del ortocentro con respecto al circuncentro O. También se dice que L (punto de Longchamps) es el pivote de la curva isoconjugada Σ(O que Σ es una cúbica pivotal isoconjugada).

Apartado 7

¿Cómo cambia el lugar Σ en el caso de que ABC sea un triángulo isósceles?

figura 9

Cuando el triángulo ABC es isósceles, por ejemplo AB y CA son los lados iguales, los puntos A, L, O, I, H, I_a de la curva de tercer orden Σ están sobre la mediatriz del lado BC, lo que indica que el lugar Σ es una curva de tercer orden que comprende una recta y por ende una cónica.

La cónica pasará por B y C, y por la simetría central tendrá por asíntotas las mediatrices a AB y BC que son perpendiculares a los lados y pasan por O.

Como comprobación analítica introducimos cosB=cosC

figura 10

En el caso que el triángulo ABC fuera equilátero, no habría ningún vértice privilegiado y por lo tanto la curva de tercer orden degeneraría en las tres mediatrices.

Como comprobación analítica introducimos cosA=cosB=cosC=½