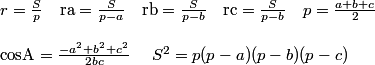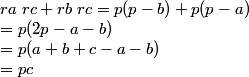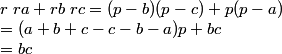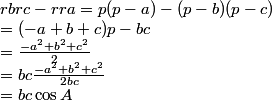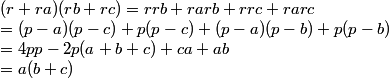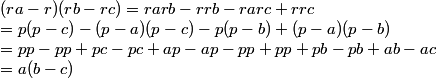Problema 477. De investigación. Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (València).

Sean r el radio de la circunferencia inscrita, ra , rb, rc radios de las circunferencias ex-inscritas, p el semiperímetro del triángulo ABC. Probar que:

a) ra +rb=(pc)/rc

b) bc=rra + rbrc

c) rbrc- rra =bc cos A.

d) a(b+c)=(r+ra)( rb+rc).

e) a (b-c)=(ra-r) ( rb-rc).

E. Lemoine (1900). Téorèmes et resultats de la géométrie del triangle. página 103, problemas 6, 23, 25, 22.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (3 de julio de 2008)

Empecemos recordando la expresión del área del triángulo en función de los distintos radios de los círculos inscritos y exinscritos y la fórmula de Herón

y recordamos también la expresión de cosA y del semiperímetro además de despejar las expresiones de los distintos radios y calcular el cuadrado del área.

y calcularemos los siguientes resultados intermedios

y análogamente

APARTADO a)

APARTADO b)

APARTADO c)

APARTADO d)

APARTADO e)