Problema 477.- (Propuesto por Ricard Peiró i Estruch. I.E.S. Abastos, Valencia).

Sean r el radio de la circunferencia inscrita, radios de las circunferencias exinscritas, p el semiperímetro del triángulo ABC. Probar que:

(a)

(b)

(c)

(d)

(e)

E. Lemoine (1900). Téorèmes et resultats de la géométrie del triangle. página 103, problemas 6, 23, 25, 22.

Resolución de Vicente Vicario García, I.E.S. El SUR, Huelva (2 de julo de 2008)

Utilizaremos la notación habitual en la geometría del triángulo, y de nuevo, emplearemos s para el semiperímetro. Escribiremos inicialmente una serie de expresiones muy conocidas relacionadas con los radios de las circunferencias exinscritas a un triángulo y deduciremos otras relaciones a partir de ellas, las cuales necesitaremos en las demostraciones de cada uno de los apartados anteriores. Comencemos con las expresiones clásicas del área del triángulo, en función de sus lados (Fórmula de Herón), y en función de los radios de las circunferencias exinscritas.

a

[1]

A partir de aquí, es sencillo demostrar las relaciones siguientes

, [2]

Por otra parte, emplearemos una serie de expresiones que aparecieron en la resolución del problema 470 de esta revista, en el que se pedía la expresión de las longitudes de los lados de un triángulo en función de los radios de las circunferencias exinscritas al mismo. Basta con plantear y resolver (como allí se indicó) el sistema, a partir de las expresiones de [1]

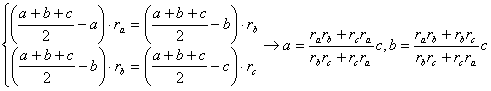
y de la relación para , obtenida con la fórmula de Herón, después de sustituir y efectuar algunas simplificaciones algebraicas, se llega a la expresión de c

y, por simetría, a la de los otros dos lados. Resulta, finalmente que

, , [3]

Iniciemos las demostraciones de cada uno de los apartados del problema

(a) . Tenemos la siguiente cadena de identidades

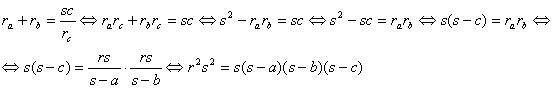
donde se han aplicado las expresiones [1] y [2] y la última expresión es la fórmula de Herón.

(b) . Utilizando las expresiones de [1] obtenemos sucesivamente

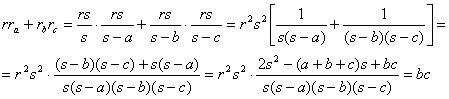
(c) . A partir del teorema de los cosenos aplicado al triángulo ABC, y de las expresiones [3] tenemos que

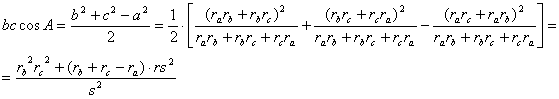donde hemos empleado la expresión [2]. Tenemos que demostrar entonces que

Y, finalmente, sustituyendo r de [1] y de [2], llegamos a una identidad algebraica que demuestra el apartado pedido

(d) . Para este apartado utilizaremos las expresiones [3]

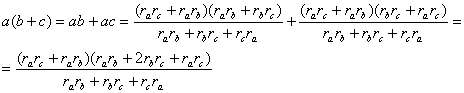
y tenemos entonces que demostrar que

que se demuestra inmediatamente sin más que sustituir por

en la expresión anterior y comprobar que tenemos una identidad algebraica. Después de sustituir y simplificar, nos queda

que, efectivamente, es una identidad.

(e) . Procediendo de forma análoga al caso anterior tenemos que

y sustituyendo , en el segundo miembro nos queda, que el apartado queda demostrado si la siguiente es una identidad

que, efectivamente, lo es.