Problema 2. (Propuesto por Vicente Vicario García, I.E.S.
El Sur, Huelva).
Sea ABC un
triángulo donde el mayor de sus ángulos no supera 120º y sea ![]() el área del mismo.
el área del mismo.
(a) Hallar el valor mínimo,
exclusivamente en función de los lados a,
b, c del triángulo, de la suma ![]() , siendo P un punto
interior al mismo.
, siendo P un punto
interior al mismo.
(b) Demostrar la desigualdad ![]() .
.
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
(a) Utilizaremos la notación habitual en la geometría del triángulo. Consideremos el triángulo ABC y los triángulos equiláteros exteriores BCA´, ACB´, ABC´ erigidos sobre los lados del mismo. Es bien conocido que las longitudes AA´, BB´ y CC´ tienen la misma longitud y además representan la longitud mínima que buscamos. Además el punto de corte de las rectas AA´, BB´ y CC´ es el punto de Fermat del triángulo, que, puesto que por hipótesis, el mayor de los ángulos del triángulo no supera a 120º, estará situado en el interior del mismo y abarcando arcos de 120º con cada uno de los lados del triángulo.
Determinemos la longitud mínima, a partir, por ejemplo, de BB´, en función exclusiva de los lados del triángulo. Para ello utilizaremos el teorema de los cosenos aplicado al triángulo BCB´, y expresiones clásicas para el área del triángulo, junto con propiedades y razones trigonométricas elementales, teniéndose que
 [1]
[1]
donde ![]() es el área del triángulo.
Finalmente, utilizando la fórmula de Herón para el área del triángulo, que
podemos expresar en la forma
es el área del triángulo.
Finalmente, utilizando la fórmula de Herón para el área del triángulo, que
podemos expresar en la forma
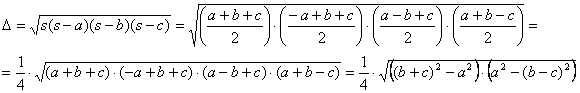
y sustituyendo en la expresión [1] y simplificando después, tenemos que

(b) Para demostrar la desigualdad pedida basta con observar la expresión [1] anterior y utilizar la conocida desigualdad de Weitzenböck
![]()
obteniéndose entonces que
![]()
Nota: Podemos observar que si en lugar de la desigualdad de Weitzenböck usamos la más refinada desigualdad de Finsler-Hadwiger
![]()
obtendríamos una desigualdad obviamente más precisa que la anterior
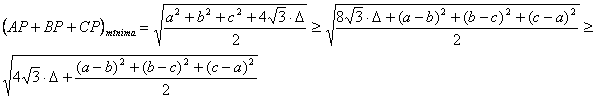
Otras estimaciones, no tan precisas, se pueden obtener a partir de la desigualdad entre las medias aritmética y geométrica de términos positivos.
---oooOooo---