Para el aula

Problema 479

25.- Construir un triángulo ABC conociendo la altura BD y los radios de las circunferencias circunscritas a los triángulos ABD y CBD.

Alexandroff, I. (1899) Problemas de geometría elemental agrupados según los métodos a emplear para su resolución. Traducido del ruso al francés, según la sexta edición por D. Aitoff. París. (p. 22)

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fenlabrada

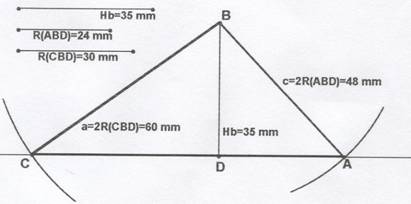
Con los tres datos de un triángulo de vértices CBD (lado CB, ángulo D opuesto al lado BC, y el radio de la circunferencia circunscrita)  se pueden conseguir tres parejas de datos equivalentes o sea con dos de estos datos se puede obtener el tercero. En este caso particular se conoce el ángulo D, que es recto por ser el pie de la altura Hb, y, el radio R(CBD) de la circunferencia circunscrita al triángulo CBD luego se podrá deducir el lado BC. La deducción del lado BC es inmediata porque la hipotenusa de un triángulo rectángulo inscrito en una circunferencia es el diámetro de la misma por ser el arco capaz de 90º del segmento BC. En conclusión el diámetro de la circunferencia circunscrita al triángulo CBD es el lado BC.

Del mismo modo el lado BA es el diámetro de la circunferencia circunscrita al triángulo ABD.