Construir un triángulo ABC conociendo la altura BD y los radios de las circunferencias circunscritas a los triángulo , .

Alexandroff, I. (1899)  Problemas de geometría elemental agrupados según los métodos a emplear para su resolución. Traducido del ruso al francés, según la sexta edición por D. Aitoff. París. (p. 22)

Solución: de Ricard Peiró i Estruch:

Sea  el radio de la circunferencia circunscrita al triángulo .

Sea  el radio de la circunferencia circunscrita al triángulo .

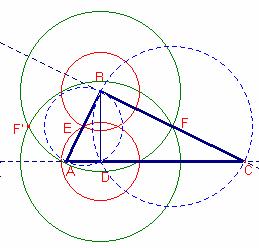
Notemos que los triángulos ,  son rectángulos, los centros

de las circunferencias circunscritas están en el punto medio de las hipotenusas.

Esta propiedad es la que nos dará la posibilidad de resolver el problema:

Construcción:

a) Dibujar el segmento .

b) dibujemos la recta r que perpendicular al segmento  que pasa por D

c) Dibujar la circunferencia de centro B y radio .

d) Dibujar la circunferencia de centre D y radio .

e) Sean las intersecciones de las dos circunferencias F, F’

Notemos que el problema tendrá dos soluciones.

f) Dibujemos la recta s que pasa por los puntos B, F.

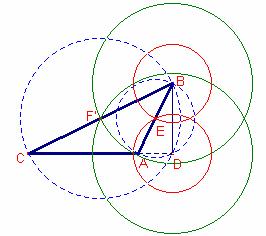g) Sea C la intersección de las rectas r, s

h) Notemos que .

i) Dibujar la circunferencia de centro B y radio .

j) Dibujar la circunferencia de centro D y radio .

k) Sean las intersecciones d’e las dos circunferencias E.

l) Dibujemos la recta t que pasa por los puntos B, E.

m) Sea A la intersección de las rectas r, t.

n) Dibujemos el triángulo .

Con Cabri:

Figura barroso479.fig

Applet created on 2/07/08 by Ricard Peiró with CabriJava