Homenaje a dos matemáticos españoles

Problema 492

Ejemplo 4.- Construir un triángulo dado el perímetro 2p, un ángulo B y el radio r’ del círculo inscrito.

Metodología y didáctica de la matemática elemental : para uso de los alumnos de Escuelas Normales y aspirantes al profesorado de 1a y 2a enseñanza / por J. Rey Pastor y P. Puig Adam Madrid [s. n.], 1933(p.83-84)

Solución tomada de los autores

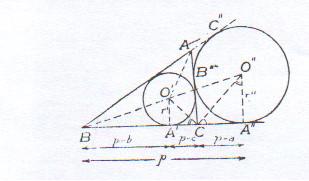
Según una propiedad conocida por Geometría, el segmento BA’’ comprendido entre un vértice B y el punto A’’ de contacto del círculo exinscrito interior al ángulo B con uno de sus lados es igual al semiperimetro p, en este caso conocido.Es decir, BA’’=BC’’=p.

<

Los datos del problema permiten, pues, construir el ángulo B, la circunferencia O’ inscrita en él, de radio dado, r’, y la exinscrita O’’ tangente en A’’ y C’’ a sus lados. Con lo cual quedará determinado el lado AC del triángulo, que será tangente común a ambas circunferencias.

El lector completará fácilmente la discusión. ¿Existe siempre solución? Cuando hay dos tangentes interiores, ¿Hay en rigor dos soluciones?