Problema 481

Sea un triángulo ABC de ángulos <BAC= 20, <ABC=120.

Sea D un punto interior tal que <BDC=50, <BAD=10.

Hallar <ABD.

Rodríguez, W. (2008): Comunicación personal.

Solución del director

Sea la figura :

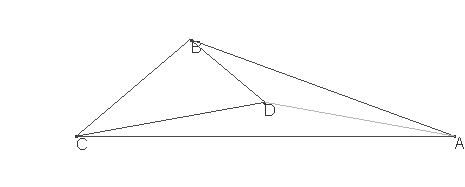
Es: <ABD=x, <ADB=170-x, <ADC= 140+x, <ACD=30-x, y así, tenemos:

CD / sen 10 = AD/ sen (30-x), DB / sen 10 =AD / sen x.

CD=(AD sen 10)/sen (30-x), DB = (AD sen 10) / sen x. [1]

En el triángulo CBD, tenemos: <BCD= 10 + x, <CBD= 120 – x .

Así, BD / sen (10 + x) = CD / sen (120 – x). [2]

De [1] y [2], se tiene: sen x sen (10 + x) = sen (30 –x) sen (120 –x). [3]

Usando la identidad trigonométrica sen x sen y = ½ [cos (x – y) - cos (x + y)] , [3] queda así:

½ [cos (-10) – cos (10+2x) ] = ½ [cos (-90) – cos (150 – 2x)]

O sea: cos 10 = cos (10 + 2x) – cos (150 – 2x).

Es decir, cos 10 = –2 sen 80 sen (2x – 70).

O sea, sen (2x – 70) = - 1/2 . 2x - 70 = -30, x=20.

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla.