Problema 481. Propuesto por William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú.

Sea un triángulo ABC de ángulos <BAC= 20, <ABC=120. Sea D un punto interior tal que <BDC=50, <BAD=10. Hallar <ABD.

Rodríguez, W. (2008): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de septiembre de 2008)

Solución

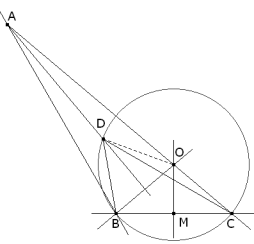
Si tazáramos el triángulo según los datos del enunciado, como el ángulo BAC es de 20º y el ángulo BAD es de 10º, deducimos que AD es la bisectriz del ángulo BAC.

Como el ángulo BDC es de 50º, deducimos que D, además de estar sobre esa bisectriz, está sobre el arco capaz de cuerda BC y ángulo de 50º.

Para hallar el centro del círculo que nos da el arco capaz, tomaremos por C una recta que forme 50º con BC y luego por C una perpendicular a esta última recta; pero el ángulo BCA es

lo que nos indica que dicha perpendicular es el propio lado CA y por lo tanto el centro O del círculo buscado está en la intersección de la mediatriz a BC y el lado AC.

Ahora bien, como el ángulo (en el centro) COB es doble que el ángulo inscrito, tenemos que el ángulo es de 2·50º=100º, lo que a su vez nos indica que el ángulo AOB es de 80º y de aquí obtenemos

Lo que nos indica que el triángulo BAO es isósceles y como AD es la bisectriz de ese triángulo, será la mediatriz de BO y por lo tanto, al estar D en esa mediatriz, el triángulo BDO es isósceles con DB=DO; pero como OD=OB por ser radios del mismo círculo nos queda que OD=DB=BO y por lo tanto el triángulo BDO es equilátero.

Si el triángulo BDO es equilátero, el ángulo DBO es de 60º y en consecuencia.