Problema 481.- (Propuesto por William Rodríguez Chamache, profesor de geometría de la “Academia integral class”, Trujillo, Perú).

Sea un triángulo ABC de ángulos , . Sea D un punto interior tal que , . Hallar .

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Utilizaremos la notación habitual en la geometría del triángulo y, sin pérdida de generalidad, supondremos que . Evidentemente se tiene que . Aplicando el teorema de los senos al triángulo ABC tenemos que

[1]

Aplicando de nuevo el teorema de los senos sucesivamente a los triángulos ABD y BDC, denotando , y teniendo en cuenta las relaciones entre ángulos suplementarios, tenemos que

[2]

[3]

donde en [3] hemos empleado la relación [1]. Igualando las expresiones para BD, es decir, las relaciones [2] y [3], tenemos la expresión que permite determinar .

[4]

Teniendo en cuenta la identidad trigonométrica y las relaciones entre ángulos complementarios, la expresión anterior se reduce a

[5]

Finalmente, demostraremos que la única solución de la ecuación trigonométrica anterior, compatible con nuestro problema es . Para ello, basta con demostrar que se cumple la relación

[6]

Para demostrarla, observemos que claramente se tiene que

[7]

[8]

Por otra parte, a partir del teorema de De Môivre, o bien, a partir de la identidad que se obtiene como

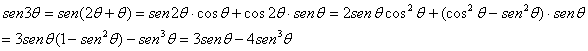
y sustituyendo , se llega a la identidad

[9]

Multiplicando [7] y [8] para obtener y teniendo en cuenta la identidad [9], se llega finalmente a

lo que demuestra lo requerido.

---oooOooo---