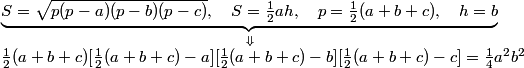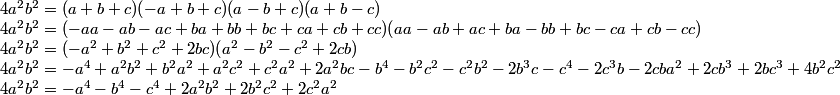Problema 482. Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva.

Demostrar que a partir de la fórmula (teorema) de Herón para el área de un triángulo se pueden deducir como corolarios el teorema de Pitágoras y su recíproco.

Nota: Existen demostraciones geométricas del teorema de Herón que no recurren en su demostración, ni al teorema de Pitágoras, ni a su teorema recíproco. Tales son, por ejemplo, la propia demostración de Herón de la proposición I.8 de su Metrica o la demostración de Euler en su artículo Variae demonstrationes geometricae de 1767. Por tanto, no se produce ningún círculo vicioso en este razonamiento. No son válidas en este sentido las demostraciones trigonométricas de la fórmula de Herón que llevan implícita en su trigonometría la relación pitagórica fundamental.

Vicario, V. (2008): Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de septiembre de 2008)

Solución

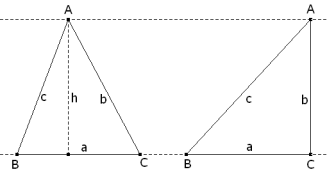
La fórmula de Herón expresa el área del triángulo en función de los lados a=BC, b=CA, c=AB y el semiperímetro p= ½ (a+b+c) del triángulo ABC

.

La fórmula del área de un triángulo nos dice que el área es igual al semiproducto de la base por la altura correspondiente

.

En el caso de que el triángulo sea rectángulo, una base y su altura coinciden con los catetos a y b = h. Si expresamos, en estas condiciones, la igualdad en las fórmulas que expresan (para evitar raíces cuadradas) el cuadrado del área del triángulo, obtenemos

Simplificando obtenemos

y desarrollando

y llevando todos los términos que contienen a c a un mismo lado de la igualdad

simplificando y ordenando

que nos proporciona

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

En general, la igualdad de cuadrados de áreas (ver ecuaciones anteriores) nos lleva a

y de aquí, Recíprocamente, si se cumple lo anterior,

que desarrollado queda como

y simplificando

por lo que

así que, como la altura h es perpendicular a la base a, el lado b es perpendicular al lado a y por ello el triángulo es rectángulo

Si en un triángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, el triángulo es rectángulo.