Problema 482
Demostrar que a partir de la fórmula (teorema) de Herón para el área de un triángulo se pueden deducir como corolarios el teorema de Pitágoras y su recíproco.
Nota: Existen demostraciones geométricas del teorema de Herón que no recurren en su demostración, ni al teorema de Pitágoras, ni a su teorema recíproco. Tales son, por ejemplo, la propia demostración de Herón de la proposición I.8 de su Metrica o la demostración de Euler en su artículo Variae demonstrationes geometricae de 1767. Por tanto, no se produce ningún círculo vicioso en este razonamiento. No son válidas en este sentido las demostraciones trigonométricas de la fórmula de Herón que llevan implícita en su trigonometría la relación pitagórica fundamental.
Vicario, V. (2008): Comunicación personal
Solución
de Ricard Peiró.
Demostración
Teorema Pitágoras:
Sea
el triángulo rectángulo 
, 
.
La
fórmula d’Heró es 
, donde 
.
En
un triángulo rectángulo 
, donde r es el radio de la circunferencia inscrita.
En cualquier
triángulo el área es 
.
En
un triángulo rectángulo el área es 
.
. Elevando al cuadrado.
.
.
. Simplificando:
.
Demostración
Teorema recíproco de Pitágoras:
En cualquier
triángulo 
.
Supongamos
que en el triángulo . Queremos demostrar que el triángulo es rectángulo.
En cualquier
triángulo el área es 
.
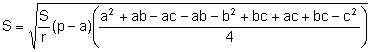. Simplificando:
. Elevando al cuadrado:
.
. Simplificando:
. Aplicando la fórmula trigonométrica del ángulo doble:
.
, 
.
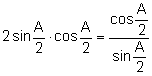. Entonces, , por tanto el triángulo es rectángulo.