Problema 1.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva).

Demostrar que a partir de la fórmula (teorema) de Herón para el área de un triángulo se pueden deducir como corolarios el teorema de Pitágoras y su recíproco.

Nota: Existen demostraciones geométricas del teorema de Herón que no recurren en su demostración, ni al teorema de Pitágoras, ni a su teorema recíproco. Tales son, por ejemplo, la propia demostración de Herón de la proposición I.8 de su Metrica o la demostración de Euler en su artículo Variae demonstrationes geometricae de 1767. Por tanto, no se produce ningún círculo vicioso en este razonamiento. No son válidas en este sentido las demostraciones trigonométricas de la fórmula de Herón que llevan implícita en su trigonometría la relación pitagórica fundamental.

Resolución: Utilizaremos la notación habitual en la geometría del triángulo, planteando el teorema de Herón como punto de partida:

Teorema (Herón): “En todo triángulo de lados a,b,c y área , tenemos que donde s es el semiperímetro del triángulo”.

Demostraremos que el teorema de Herón resulta ser teorema globalizador no sólo del teorema de Pitágoras sino también de su teorema recíproco. En la demostración de Herón (o en la de Euler) no se invoca al teorema de Pitágoras ni a su teorema recíproco, siendo ésta una demostración relativamente extensa, en la que aparecen con profusión una serie de relaciones de semejanza entre triángulos que se encajan finalmente en la deducción final. Por tanto, los teoremas de Pitágoras y su recíproco son casos particulares del teorema de Herón que es mucho más general y rico que sus teoremas aplicados. Veamos a continuación cómo obtener el teorema de Pitágoras y su recíproco como corolarios del teorema de Herón.

Teorema de Pitágoras: (Corolario del teorema de Herón)

Demostración: Sea un triángulo rectángulo con hipotenusa de longitud a y catetos de longitudes b y c. El semiperímetro del triángulo será entonces . De forma análoga obtenemos , , .

Por otra parte, tras manipulaciones algebraicas llegamos a la expresión siguiente

Si insertamos estos valores en la expresión relativa al teorema de Herón y sustituimos el valor para el área del triángulo rectángulo (catetos b, c) se obtiene

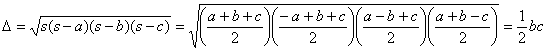
que elevando al cuadrado, reordenando y simplificando nos lleva a las relaciones

que es la relación del teorema de Pitágoras.

Teorema recíproco al de Pitágoras: (Corolario del teorema de Herón)

Demostración: Sea un triángulo tal que siendo a, b, c las longitudes de sus tres lados se verifique la relación . Utilizando entonces el teorema de Herón y designando s como el semiperímetro del triángulo tenemos, después de las manipulaciones algebraicas realizadas anteriormente

donde h es la altura del triángulo relativa a la base de longitud b del mismo. Entonces sustituyendo por , operando, reordenando y simplificando tenemos

que nos dice que el triángulo debe ser rectángulo ya que la longitud de la altura relativa al lado de longitud b es precisamente de valor a.

Como podemos percibir, el teorema de Pitágoras y su recíproco surgen y son demostrados de esta manera sin ninguna aparente vinculación entre ambos. Euclides en las proposiciones finales 47 y 48 del libro I de los Elementos demostró el teorema recíproco al de Pitágoras utilizando en su argumentación el propio teorema de Pitágoras o teorema directo. Aquí surgen como simples aplicaciones o corolarios del teorema de Herón.