Problema 483
En un triangle rectangle 
, 
es traça 
perpendicular a 
i també 
i 
, bisectrius dels angles 
i 
, respectivament.
Demostreu que:
a) La bisectriu de l’angle B és perpendicular a 
i la bisectriu de
l’angle B és perpendicular a 
. A més a més, és bisecat per la
bisectriu de l’angle B (en un punt a),i és bisecat per la
bisectriu de l’angle A (en un punt b) i conseqüentment 
és paral·lel a i igual a 
.
b) Les bisectrius 
tallen la hipotenusa en segments 
que són iguals als
costats 
, respectivament.
c) L’inradi de és 
.
d) Si c i d són els incentres de 
i 
. 
, és a dir, r és el costat del quadrat de diagonal 
.
e) La recta que passa pels incentres de i és perpendicular a la
bisectriu de C, és a dir, és perpendicular a la
bisectriu 
.
f) Els punts c i d equidisten de la projecció de l’incentre de en .
Babbit, A. (1918) AMM. Pp. 347-348. Los apartados
(g) y (h) son del profesor J. B. Romero Márquez.
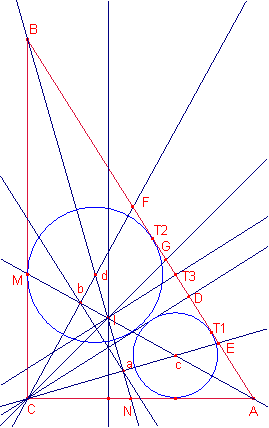Solució
de Ricard Peiró:
Siguen 
els costats del
triangle .
Siga 
.
a)
, 
, aleshores, 
i són perpendiculars.
, 
, aleshores, 
i són perpendiculars.
Aplicant la propietat de la bisectriu a :
. Aleshores, 
Aplicant raons trigonomètriques al triangle rectangle 
:
(1)
Aplicant el teorema dels sinus al triangle 
:
.
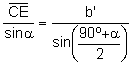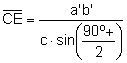(2)
Dividint les expressions (1) i (2):
Per tant, és bisecat per la
bisectriu de l’angle B. 
Anàlogament, és bisecat per la
bisectriu de l’angle A,
.
Notem que és paral·lela mitjana
del triangle 
. Aleshores, 
.
b)
, 
, aleshores el triangle 
és isòsceles, per
tant, 
.
Anàlogament, el triangle 
és isòsceles, 
.
c)
Siga r l’inradi del triangle per ser el triangle
rectangle, 
.
Aleshores, .
d)
Aplicant el teorema del catet i de l’altura al triangle
rectangle :
, 
, 
.
Siga 
els inradis dels triangles
rectangles i , respectivament.
Aleshores, 
, 
.
Siga 
la projecció del
centre c sobre la hipotenusa .
Siga 
la projecció del
centre d sobre la hipotenusa .
Per ser , punts de tangència de les circumferències inscrites:
, 
.
.
Aleshores,
.
Aleshores, 
.
Per tant, .
e)
Considerem el triangle 
.
Siga del centre I
incentre del triangle .
és altura del triangle
.
és altura del triangle
.
Les dues altures s’intersecten
en l’incentre I, ortocentre del triangle .
Aleshores, la recta CI és altura del triangle .
Per tant, és perpendicular a la
bisectriu .
f)
Siga 
la projecció del
centre I incentre del triangle sobre la hipotenusa .
Per ser punt de tangència de
la circumferència inscrita al triangle .
, 
.
.
.
Aleshores, els punts c i d equidisten de la projecció de l’incentre de en .