Problema 483

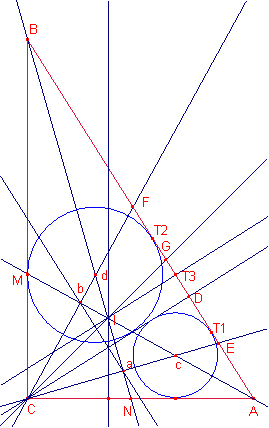
En el triángulo rectángulo ABC (con el ángulo recto en C), se traza CD perpendicular a AB, y también CE, CF, BM y AN, bisectrices de los ángulos ACD, BCD, ABC y CAB respectivamente.

Demostrar que:

a)     La bisectriz del ángulo B es perpendicular a CE, y la bisectriz del ángulo A es perpendicular a CF. Además, CE es bisecado por la bisectriz del ángulo B (en un punto a), y CF es bisecado por la bisectriz del ángulo A (en un punto b), y consecuentemente ab es paralela a AB e igual a ½ EF.

b)      Las bisectrices CF y CE cortan a la hipotenusa AB en segmentos AF y BE que son iguales a los lados AC y BC respectivamente.

c)     El inradio de ABC es 1/2EF=ab.

d)      c y d son los incentros de ADC y BDC. r=cd/sqr(2), es decir, r es el lado del cusdrado cuya diagonal es cd.  

e)      La recta de los incentros de los triángulos ADC y BDC es perpendicular a la bisectriz de C, es decir, cd es perpendicular a CG.

f)       c y d equidistan de la proyección del incentro de ABC a AB

Babbit, A. (1918) AMM. Pp. 347-348. Los apartados (g) y (h) son del profesor J. B. Romero Márquez.

Solución de Ricard Peiró:

Sean els lados del triángulo .

Sea .

a)

, , entonces, i son perpendiculares.

, , entonces, i son perpendiculares.

Aplicando la propiedad de la bisectriz a :

. Entonces,

Aplicando razones trigonométricas al triángulo rectángulo :

(1)

Aplicando el teorema de los senos al triángulo :

.

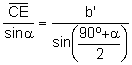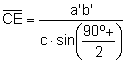(2)

Dividiendo las expresiones (1) y (2):

Por tanto, está bisecado por la bisectriz del ángulo B.

Análogamente, está bisecado por la bisectriz de l’ángulo A,

.

Notemos que es paralela media del triángulo . Entonces, .

b)

, , entonces el triángulo es isósceles, por tanto, .

Análogamente, el triángulo es isósceles, .

c)

Sea r el inradio del triángulo por ser el triángulo rectángulo, .

Entonces, .

d)

Aplicando el teorema del cateto y de la altura al triángulo rectángulo :

, , .

Sea los inradios de los triángulos rectángulos i , respectivamente.

Entonces, , .

Sea la proyección del centro c sobre la hipotenusa .

Sea la proyección del centro d sobre la hipotenusa .

Por ser , puntos de tangencia de las circunferencias inscritas:

, .

.

Entonces,

.

Entonces, .

Por tanto, .

e)

Consideremos el triángulo .

Sea del centro I incentro del triángulo .

es altura del triángulo .

es altura del triángulo .

Las dos alturas se intersectan en el incentro I, ortocentro del triángulo .

Entonces, la recta CI es altura del triángulo .

Por tanto, es perpendicular a la bisectriz .

f)

Sea la proyección del centro I incentro del triángulo sobre la hipotenusa .

Por ser punto de tangencia de la circunferencia inscrita al triángulo .

, .

.

.

Entonces, los puntos c y d equidistan de la proyección del incentro de en .