Problema 483.- (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid).

En el triángulo rectángulo ABC (con el ángulo recto en C), se traza CD perpendicular a AB, y también CE, CF, BM y AN bisectrices de los ángulos ACD, BCD, ABC y CAB respectivamente. Demostrar que:

(a) La bisectriz del ángulo B es perpendicular a CE y la bisectriz del ángulo A es perpendicular a CF. Además, CE es bisecado por la bisectriz del ángulo B (en un punto P), y CF es bisecado por la bisectriz del ángulo A (en un punto Q), y consecuentemente PQ es paralelo a AB e igual a ½ de EF.

(b) Las bisectrices CF y CE cortan a la hipotenusa AB en segmentos AF y BE que son iguales a los lados AC y BC respectivamente.

(c) El inradio de ABC es ½ de EF e igual a PQ.

(d) R y S son los incentros de ADC y BDC, , es decir, es el lado del cuadrado cuya diagonal es RS.

(e) La recta de los incentros de los triángulos ADC y BDC es perpendicular a la bisectriz que parte de C, es decir, RS es perpendicular a CG.

(f) R y S equidistan de la proyección del incentro de ABC respecto de AB

(g) Todas las proposiciones anteriores son lógicamente equivalentes.

(h) ¿Cualquiera de ellas caracteriza de forma unívoca a los triángulos rectángulos? Esto es, en cualquier otro triángulo no rectángulo se tendrá que las desigualdades dadas aquí se convertirán en una desigualdad para un lado u otro según el tipo de triángulo que estemos considerando: acutángulo u obtusángulo.

Babbit, A. (1918) AMM. Pp. 347-348. Los apartados (g) y (h) son del profesor J. B. Romero Márquez.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Sin pérdida de generalidad supondremos que . Supondremos efectuadas las construcciones del problema.

(a) Puesto que el triángulo ABC es rectángulo en C, es claro que y . Entonces tenemos que

De forma análoga, puesto que , tenemos que

y esto demuestra que y .

Pasemos ahora a demostrar que CE es bisecado por BM en el punto P y que CF es bisecado por AN en e punto Q. Utilizaremos el hecho bien conocido (que se obtiene por semejanza de triángulos) que asegura que y las expresiones clásicas para las longitudes de las bisectrices interiores en un triángulo , etc. Por otra parte, por el teorema de las bisectrices interiores, se tiene

Por otra parte, los triángulos MPC y CED son semejantes por ser rectángulos y tener un ángulo agudo común. Podemos plantear entonces que

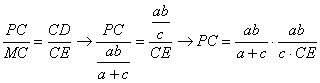[1]

Además, utilizando la expresión de la longitud de la bisectriz llegamos a

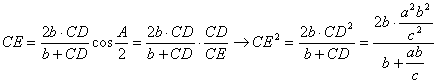
de forma que después de simplificar llegamos a 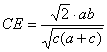. Entonces sustituyendo CE en la expresión [1], finalmente tenemos que

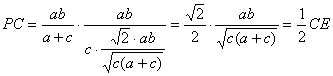
lo que demuestra que BM biseca a CE. De forma totalmente análoga se demuestra que AN biseca a CF. Para ello basta con observar que los triángulos CQN y CDF son semejantes y proceder de la misma forma que anteriormente. En consecuencia en el triángulo ECF se tiene que PQ es paralela media y mide la mitad que el segmento EF.

(b) Demostraremos que las bisectrices CF y CE cortan a la hipotenusa AB en segmentos AF y BE que cumplen y .

Consideremos el triángulo ACF. Es claro que , y que además . Por tanto, , y en consecuencia, el triángulo ACF es isósceles con como se requería.

De forma análoga, en el triángulo BEC se tiene que , y además

se tiene que . Por tanto tenemos que , y en consecuencia, el triángulo BEC es isósceles con .

(c) Demostraremos ahora que el inradio del triángulo ABC es la mitad de EF, y por tanto, igual a PQ.

Determinemos primero el valor del inradio del triángulo ABC a partir de la fórmula del área del mismo

ya que puesto que .

Por otra parte, tenemos que

con lo que se tiene la demostración pedida.

(d) Demostraremos que si R y S son los incentros de los triángulos ADC y BDC respectivamente, entonces se tiene para el inradio de ABC la relación siguiente , es decir, r es el lado del cuadrado cuya diagonal es RS.

Utilizaremos la expresiones bien conocidas , y , que se deducen de los teoremas de la altura y el cateto aplicados al triángulo rectángulo ABC de partida. Además, sabemos que el radio de la circunferencia inscrita a un triángulo rectángulo se determina como la mitad de la diferencia entre la suma de los catetos y la hipotenusa. Por tanto, es claro que

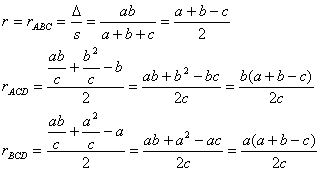
Por otra parte, podemos suponer, sin pérdida de generalidad que con lo que se tiene . Aplicando el teorema de Pitágoras podemos determinar la distancia entre los incentros respectivos R y S de los triángulos ACD y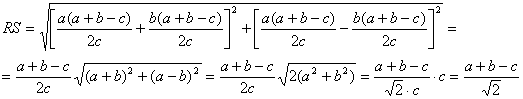

y, en consecuencia, es claro que:

(e) Demostraremos ahora que la recta RS que une los incentros de los triángulos ADC y BDC, es perpendicular a la bisectriz interior del triángulo ABC que parte del vértice C, es decir, .

De nuevo, supondremos sin pérdida de generalidad que, con lo que se tiene . Denotaremos por el ángulo que forma el segmento RS con cualquier paralela al lado AB del triángulo ABC y por el ángulo que forman la bisectriz interior CG y la altura CD del mismo. Tenemos claramente que

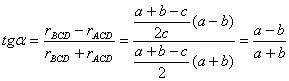
Por otra parte, tenemos que , con . Por el teorema de las bisectrices interiores aplicado al triángulo ABC, tenemos que

y, en consecuencia

y, por tanto

demostrando así que los ángulos agudos y son iguales, y la recta RS es perpendicular a la bisectriz CG.

(f) Demostraremos que los incentros R y S equidistan de la proyección del incentro de ABC sobre el lado AB.

Sea H el punto proyección del incentro I del triángulo ABC sobre el lado AB. Es bien conocido que y . Sean R´ y S´ las proyecciones de los incentros R y S sobre le mismo lado del triángulo. Entonces, es fácil ver que

Entonces, teniendo en cuenta que ABC es rectángulo, se tiene que

y, en consecuencia

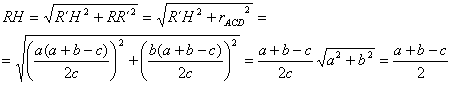
De forma análoga se tiene

y, por tanto

y finalmente

lo que demuestra la proposición.

(g) y (h). Para demostrar la veracidad o falsedad del apartado (g) analizaremos el apartado (f) primero. A lo largo de la resolución, veremos que las proposiciones (a) y (b) son proposiciones de condición necesaria y suficiente, pero no así la proposición (c) en la que el teorema recíproco (c´) no se deduce. Por tanto, NO todas la proposiciones dadas son lógicamente equivalentes y NO todas caracterizan de forma unívoca a los triángulos rectángulos.

(a´) Sea ABC un triángulo sobre el que se han definido todos lo spuntos y rectas anteriores. Demostraremos que si o si , entonces el triángulo es rectángulo en C.

Supongamos que la bisectriz del ángulo B, es decir BM es perpendicular a la bisectriz CE. Tracemos la altura CD sobre el lado AB. Es claro que , y . Puesto que , se tiene

y el triángulo ha de ser rectángulo en C. De forma análoga se demuestra en el otro caso.

(b´) Demostraremos que si las bisectrices CF y CE cortan al lado AB en segmentos AF y BE que son iguales a los lados AC y BC, respectivamente, entonces el triángulo es rectángulo en C. Para la demostración necesitamos un lema.

Lema: “En todo triángulo ABC se tiene: ”.

Demostración: Basta con observar las relaciones siguientes

■

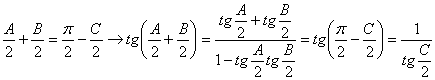Supongamos que . Es claro que

Por otra parte, también es fácil observar que

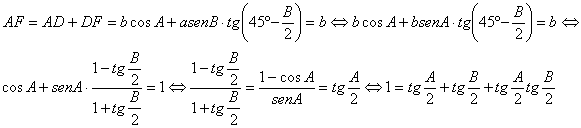
y, teniendo en cuenta la última relación junto con el lema anterior, se llega a

.

y el triángulo ABC es rectángulo en C. De forma análoga se demuestra en el caso de .

(c´) Intentaremos demostrar aquí que si en un triángulo ABC, (con las construcciones previas del problema) se tiene que el inradio del mismo es igual a la mitad del segmento EF, entonces el triángulo es rectángulo en el vértice C. Como tendremos ocasión de ver, en este apartado, NO tenemos una implicación lógica como la que tuvimos en los dos apartados anteriores (a´) y (b´), con lo que no se deduce lógicamente la conclusión deseada. Esto implica que todas las proposiciones dadas no son lógicamente equivalentes y de todas ellas no se deduce que de su cumplimiento se tenga forzosamente un triángulo rectángulo en el vértice C.

Supongamos un triángulo ABC en el cual se tenga la relación . En virtud del teorema de las bisectrices interiores aplicado al triángulo ACD, tenemos que

De forma análoga, aplicando el mismo teorema al triángulo CBD, se tiene que

Entonces, tenemos la siguiente expresión para EF, en la que se utiliza el teorema de los senos generalizado e identidades trigonométricas elementales:

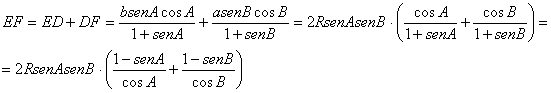
Imponiendo la condición pedida , y teniendo en cuenta que

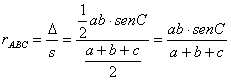
se tiene la igualdad siguiente

y, utilizando el teorema de los senos generalizado se llega a

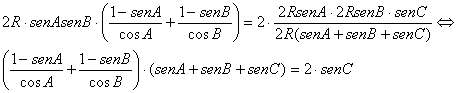
Resolviendo en la incógnita , tenemos que

que nos lleva a

y que NO implica la conclusión , ya que como se puede ver fácilmente, la igualdad entre las expresiones que configuran el numerador y el denominador de la fracción anterior, NO es una identidad trigonométrica. No obstante, es fácil ver que siempre se cumple la conclusión querida si se escogen ángulos A y B que sean complementarios entre sí, es decir, para un triángulo rectángulo. Pero esto ya lo habíamos demostrado en el apartado (c) anterior.

Además, como fácilmente se puede verificar, se tiene la igualdad entre numerador y denominador de la fracción anterior si escogemos cualquier A y , pero esto es insuficiente con , como se pretende.

---oooOooo---