Problema 484

564 Sea S el área del triángulo y S_n el área del triángulo formado por los puntos de tangencia de la circunferencia inscrita. Es:

S=S_n(2R/r)

Alasia, C. (1900): La recente geometría del triangolo. Cittá di Castello, S. Lapi, tipografo-editore. (p. 339)

Solución del editor.

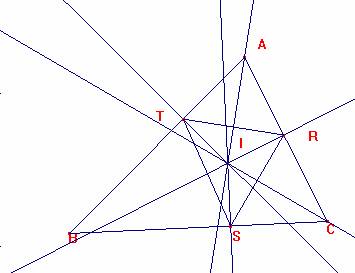
R es el circunradio de ABC.

S[ABC]=S=ah_a/2. a=2R sen A. b=2R sen B. h_a=b sen C

Así, es S=2R² sen A sen B sen C.

En el triángulo

Es <STR=90-C/2, <SRT=90-B/2, <TSR=90-A/2

r, inradio de ABC, es el circunradio de TRS.

S_n=S[TRS]=2r² sen (90- A/2) sen (90-B/2) sen (90-C/2)

S_n=2r² cos (A/2) cos (B/2) cos (C/2).

Luego es:

S/S_n = (16 R² sen A/2 cos B/2 sen B/2 cos B/2 sen C/2 cos C/2)/ (2r² cos (A/2) cos (B/2) cos (C/2))=(8 R² sen A/2 sen B/2 sen C/2 )/r²

Así, para demostrar la relación pedida, hemos de tener:r= 4R sen A/2 sen B/2 sen C/2

Sea p el semiperímetro de ABC. Es S=pr, r=S/p.

Es p=(a+b+c)/2=Rsen A+Rsen B+Rsen C=R(sen A+sen B + sen(180-(A+B)).

p= R(sen A+sen B + sen A cos B + cos A sen B).

p= R(sen A (1+cos B) + sen B (1+cos A)

p=R(2sen (A/2)cos (A/2) 2 cos² (B/2) +2sen (B/2)cos (B/2) 2 cos² (A/2))

p=4R(cos(A/2) cos(B/2) [sen (A/2) cos (B/2) + sen (B/2) cos (A/2)]

p= 4Rcos(A/2) cos(B/2) sen (A/2+B/2)

p= 4Rcos(A/2) cos(B/2) sen (90-C/2)= 4Rcos(A/2) cos(B/2) cos (C/2).

Así, r=S/p= (2R² sen A sen B sen C)/ (4Rcos(A/2) cos(B/2) cos (C/2))

r=(2R² (2sen A/2 cos B/2) (2sen B/2 cos B/2) (2sen C/2 cos C/2))/ (4Rcos(A/2) cos(B/2) cos (C/2))

r=4 R sen A/2 sen B/2 sen C/2, cqd.

Referencias:

Baker, M. (1885): A Collectio of formulǽ for the area of a plane triangle. The Annals of Mathematics, Vol. 1, No. 6 (Jan), pp. 134-138

http://www.cut-the-knot.org/triangle/RelationsInTriangle.shtml#r4R

Ricardo Barroso Campos.

Didáctica de las Matemáticas

Universidad de Sevilla.