Problema 484

564 Sea S el área del triángulo y S_n el área del triángulo formado por los puntos de tangencia de la circunferencia inscrita. Es:

Alasia, C. (1900): La recente geometría del triangolo. Cittá di Castello, S. Lapi, tipografo-editore. (p. 339)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Teniendo en cuenta el valor de los segmentos determinados en los lados por los puntos de contacto de la circunferencia inscrita, que se muestran en la figura, el lado B’C’ se calcula fácilmente en el triángulo isósceles AB’C’.

B’C’=2. Y expresiones isomorfas para otros tres lados.

La relación entre el área S de un triángulo de lados a, b y c y el radio R de la circunferencia circunscrita al mismo viene dada por la expresión S = . Aplicándola al triángulo inscrito A’B’C’ tendremos

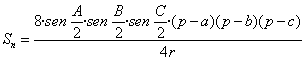(1)

Transformamos esta expresión, calculando el valor de las razones trigonométricas que en ella intervienen.

Partiendo de y del teorema del coseno , tendremos , y de ahí

y fórmulas análogas para los otros ángulos. Multiplicándolas se tiene

Aplicando todo esto a la expresión (1) y utilizando la fórmula de Herón para el área del triángulo resulta

==. (También se ha utilizado que el área es igual al producto del semiperímetro por el radio del círculo inscrito).

De esta cadena de igualdades se concluye la que buscamos: .