Problema 484.- (Propuesto por Ercole Suppa, profesor
titular de matemáticas y física del Liceo Scientifico “Albert Einstein”, 64100,
Teramo, Italia).
Sea S el área de un triángulo y
el área del triángulo formado por los puntos de tangencia de
la circunferencia inscrita. Entonces 
.
Alasia, C. (1900): La recente
geometría del triangolo. Cittá di castello, S. Lapi, tipógrafo-editore.
(p.339).
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
Demostraremos la proposición de dos formas diferentes. Utilizaremos la notación habitual en la geometría del triángulo y usaremos la notación más cómoda y usual [XYZ] para el área del triángulo XYZ.
Demostración 1ª: Denotaremos 
y 
, donde A´, B´, C´
son los puntos de tangencia de la circunferencia inscrita al triángulo ABC sobre los lados BC, AC y BA, respectivamente. Es bien conocido
que los puntos de tangencia de dicha circunferencia con los lados que parten
del vértice A están a distancia 
, y análogamente para los demás vértices, 
para el vértice B y 
para el vértice C. Podemos plantear la relación
siguiente entre áreas de triángulos
Por otra parte, es inmediato que los triángulos AC´B´, BA´C´ y CA´B´ son isósceles. Utilizando las expresiones para el área del triángulo [ABC] y sustituyendo en la expresión anterior tenemos que
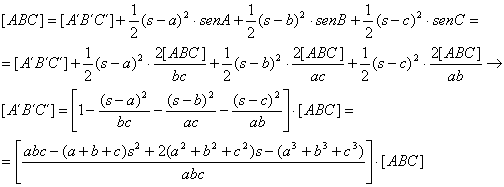
[1]
Por
otra parte, podemos determinar el valor de las expresiones del corchete en
función exclusivamente de los valores de R,
r y s del triángulo de partida ABC.
Para determinar 
, primero calculamos 
, a partir de la fórmula de Herón para el área y la famosa
relación 
. Tenemos entonces que
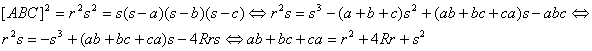
y, en consecuencia
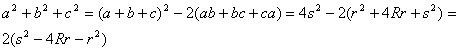
Para determinar 
haremos uso de la
identidad algebraica
con lo que empleando las expresiones anteriores, llegamos a
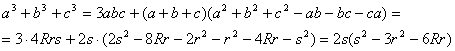
Finalmente, sustituyendo en la expresión [1] los valores anteriores, tenemos que
lo que concluye la demostración.
Nota: Observemos que podemos escribir fácilmente el cociente anterior exclusivamente en función de los lados del triángulo ABC utilizando las expresiones
y , de manera que
Demostración 2ª: En
esta demostración haremos uso de la notación anterior y partiendo del hecho
claro de que 
y 
, tenemos que
y resultado similares para los otros dos ángulos. Aplicando el teorema de los cosenos al triángulo isósceles AC´B´ llegamos a
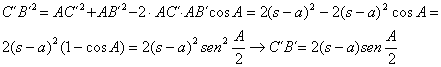
y análogamente se obtienen expresiones similares para los otros dos lados del triángulo A´B´C´. Por otra parte, son bien conocidas las expresiones
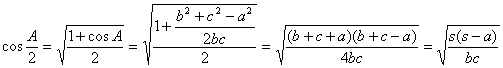
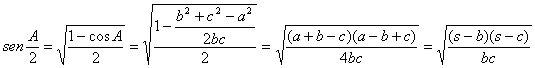
Finalmente, el área del triángulo A´B´C´ viene dada por
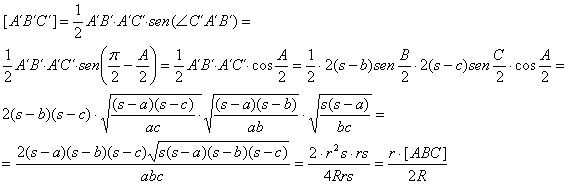
lo que concluye la demostración.