Problema 485

1.- Si els punts que divideixen cada costat d’un triangle en tres parts iguals s’uneixen al corresponent vèrtex oposat, es forma un hexàgon l’àrea del qual és la dècima part de l’àrea del triangle.

2.- Tres diagonals de l’hexàgon són segments de les mitjanes originals.

3.- L’hexàgon dóna lloc a dos triangles de costats paral·lels a l’original.

Cuoco, A. Goldenberg, P.and Mark, J.(1993). Reader Reflections. Marion´s Theorem. The Matematics Teacher, 86(8). Kennedy response.(p. 619)

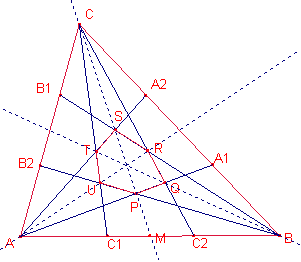
Solució de Ricard Peiró:

Siga el triangle , els costats del qual estan dividits en tres parts iguals pels punts . Al unir els punts amb els vèrtex oposats es forma l’hexàgon PQRSTU (veure figura).

Dos triangles que tenen la mateixa altura les àrees són proporcionals a les bases.

a) Vegem que els vèrtexs P, S pertanyen a la mitjana referida al vèrtex C, .

Considerem la ceviana que passa pel punt P. P és intersecció de 3 cevianes. Aplicant el teorema de Ceva:

.

, Aleshores, , aleshores, M’ és el punt mig del costat .

Per tant, P pertany a la mitjana .

Considerem la ceviana que passa pel punt S. S és intersecció de 3 cevianes. Aplicant el teorema de Ceva:

.

, Aleshores, , aleshores, M” és el punt mig del costat .

Per tant, S pertany a la mitjana .

b) Vegem que .

Siga , , , . Aleshores . .

.

Aleshores, resolent el sistema format per les 3 equacions:

, .

.

Anàlogament, .

c) Vegem que és paral·lel a

, aplicant el teorema invers del teorema de Tales:

és paral·lel a i a més a més:

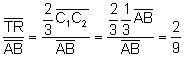
Anàlogament, és paral·lel a . és paral·lels a i en tots dos casos és la raó de semblança.

Aleshores, és semblant al triangle i és la raó de semblança.

d) Vegem que .

, . ,

Aleshores, resolent el sistema .

Aleshores, .

Anàlogament:

.

e) Vegem que és paral·lel a

, aplicant el teorema invers del teorema de Tales:

és paral·lel a i a més a més:

.

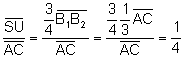Anàlogament, és paral·lel a , és paral·lel a .

Aleshores, és semblant al triangle i és la raó de semblança.

f) Vegem que .

.

.

Aleshores, .

g) Vegem que .

, .

Aleshores, .

Anàlogament, .

h) Vegem que .

.