Problema
485
1.-
Si los puntos que divide cada lado de un triángulo en tres partes iguales se
une al correspondiente vértice opuesto, se forma un hexágono el área del cual es
la décima parte del área del triángulo.
2.-
Tres diagonales del hexágono son segmentos de las medianas originales.
3.-
El hexágono da lugar a dos triángulos de lados paralelos al original.
Cuoco, A.
Goldenberg, P.and Mark, J.(1993). Reader Reflections. Marion´s Theorem. The Matematics Teacher, 86(8). Kennedy response.(p.
619)
Solución
de Ricard Peiró:
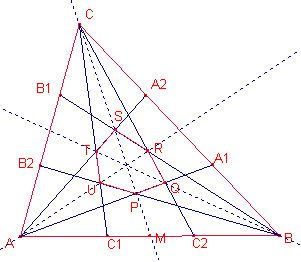Sea el triángulo
,
los lados del cual están divididos en tres partes iguales por los puntos 
.
Al unir los puntos con los vértices opuestos se forma el hexágono PQRSTU (ver
figura).
Dos
triángulos que tienen la misma altura las áreas son proporcionales a las bases.
a) Veamos
que los vértices P, S pertenecen a la mediana referida al vértice C, 
.
Consideremos
la ceviana 
que pasa por el punto
P. P es intersección de 3 cevianas. Aplicando el teorema de Ceva:
.
, Entonces, 
, entonces, M’ es el punto medio del lado 
.
Por
tanto, P pertenece a la mediana .
Consideremos
la ceviana 
que pasa por el punto
S. S es intersección de 3 cevianas. Aplicando el teorema de Ceva:
.
, Entonces, 
, entonces, M” es el punto medio del lado .
Por
tanto, S pertenece a la mediana .
b) Veamos
que 
.
Siga
, 
, 
, 
. Entonces 
. 
.
.
Entonces,
resolviendo el sistema formado por las 3 ecuaciones:
, 
.
.
Análogamente, 
.
c) Veamos
que 
es paralelo a 
, aplicando el teorema inverso del teorema de Tales:
es
paralelo a y además:
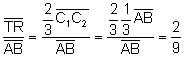
Análogamente,
es paralelo a 
. 
es
paralelo a 
y en los dos casos 
es la razón de semejanza.
Entonces,
es semejante al triángulo
y es la razón de semejanza.
d) Veamos
que 
.
, 
. 
, 
Entonces,
resolviendo el sistema 
.
Entonces, 
.
Análogamente:
.
e) Veamos
que 
es paralelo a 
, aplicando el teorema inverso del teorema de Tales:
es
paralelo a y además:
.
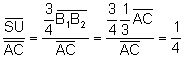Análogamente,
es paralelo a , 
es paralelo a .
Entonces,
es semejante al triángulo
i es la razón de semejanza.
f) Veamos
que 
.
.
.
Entonces, .
g) Veamos
que 
.
, 
.
Entonces, .
Análogamente, 
.
h) Veamos
que 
.
.