Problema 485.- [1] Si los puntos que
dividen cada lado de un triángulo en tres partes iguales se unen al
correspondiente vértice opuesto, se forma un hexágono cuya área es la décima
parte del área del triángulo.
Cuoco, A. Goldenberg, P.and Mark, J.(1993). Reader
Reflections. Marion´s Theorem. The
Matematics Teacher, 86(8). Kennedy response.(p. 619)
[Desde Febrero de
Teorema de Marion.
La cubierta de
Febrero de 1992 de Mathematics Teacher mostraba que si las terceras partes de
los lados de un triángulo equilátero se unían a los vértices opuestos, el
triángulo central tenía de área la séptima parte del área del triángulo
original. En una carta en Marzo de 1993, Joe Kennedy señalaba que tal restricción
a un triángulo equilátero no era necesaria [ver problema 22 de este
trianguloscabri].
Alrededor de hace
un año, Marion Walter y yo descubrimos el teorema dado, con el programa Geometer´s
Sketchpad descubrió el siguiente resultado, llamado Teorema de Marión en su
honor:
El resultado puede
ser demostrado por medios euclídeos, pero otro método de demostración es
demostrarlo en un caso especial, el equilátero, y aplicar una transformación
lineal que preserva las razones y las áreas hacia cualquier triángulo. Cuoco,
A. Goldenberg, P.and Mark, J.
Kennedy responde:
Este resultado me resulta agradable y sorprendente. Es hermoso y yo creo que el
descubrirlo utilizando tecnología es una manera apropiada. Cuoco, Goldenberg,
and Mark, dicen que lo han demostrado usando métodos ordinarios pero no lo he
visto ni he hecho intentos.
Mis precipitadas
miradas al teorema de Marion me llevan a algunas cuestiones. [2] Primero, tres
diagonales son segmentos de las medianas originales.
[3]Segundo, el
hexágono da lugar a dos triángulos de lados paralelos al original...
Nota del director
de trianguloscabri: Se observan problemas derivados... [1], [2] y [3]
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca
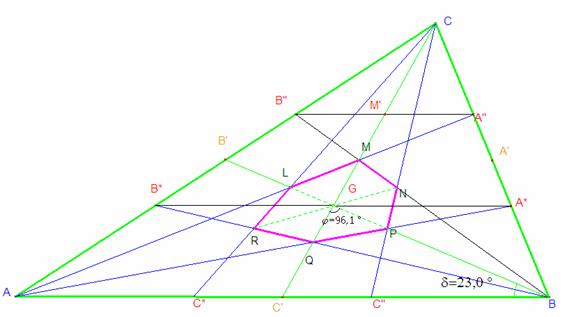
El teorema de Ceva aplicado a las cevianas concurrentes en Q, nos da que este punto se ha de encontrar sobre la mediana que parte de C. Por el mismo teorema concluimos que también M se encuentra en esa mediana. Así pues, los pares de vértices opuestos del hexágono se hallan sobre cada una de las medianas.
Vamos a tratar de caracterizar estos puntos. Comenzamos con M.
Como la razón de semejanza de los triángulos MB”A” y MAB es 1/3 la porción de mediana del primero MM’ es un tercio de la correspondiente porción del segundo, MC’.
También en los triángulos semejantes CB”A” y CAB se tiene, por igual razón, que CM’ es un tercio de la mediana CC’.
Tenemos pues: CM’=
, por tanto M’C’=
. Como MM’ es la tercera parte de MC’, MM’=
M’C’= ·=
, de ahí CM = +=
.
La conclusión tiene un enunciado sencillo:
El vértice M es el punto
medio de la mediana que sale de C, y también el punto medio del segmento GM’. Se tienen así las igualdades MM’= GM = GQ =.
De la semejanza de los triángulos
QA*B*
y QAB se deduce que QC’=
QG. Por tanto GC’== QC’+QG =QG + QG = 
y de ahí resulta QG = 
.
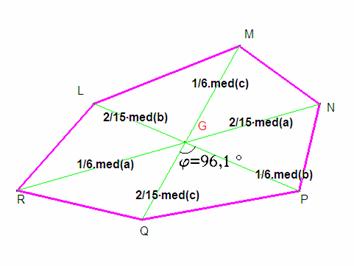
A partir de estos datos podemos
ver de inmediato que los 6 triángulos en que descompone el hexágono desde el
baricentro tienen sus áreas iguales dos a dos los que tienen vértices opuestos.
Veremos que todos, no sólo los opuestos, tienen igual área, y que ésta es 
del área de todo el
triángulo. Con esto acabará la demostración. En la figura aumentada a escala
del hexágono hemos puesto las medidas de los lados de estos seis triángulos.
Usaremos para el área de un triángulo la expresión Área(XYZ)=1/2· yx·sen X. Vamos a aplicarla al triángulo GPQ.
Observando el triángulo ABB’, aplicando la ley de los senos podemos poner
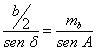
Fijándonos ahora en C’BG, otra vez por el teorema de los senos escribimos
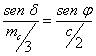
Multiplicándolas entre sí, eliminamos el valor de sen d, y podremos despejar el valor sen j que necesitamos para calcular el área del triángulo GPQ.
Se
tiene senj = 
=
donde S designa
el área del triángulo ABC. Entonces:
Área(GPQ) = 
=
El procedimiento es igualmente válido para cualquiera de los
otros cinco triángulos que componen el hexágono, con lo que queda probado que
el área de éste último es la décima parte de la del triángulo de partida, como
se pretendía probar.