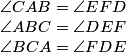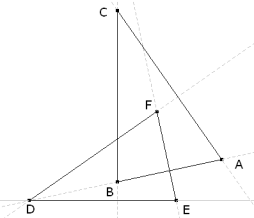
Problema 486. Sean dos triángulos ABC y DEF tales que AB es perpendicular a EF, BC perpendicular a DE y CA es perpendicular a FD . Demostrar que los triángulos ABC y DEF son semejantes.

XI Olimpiada de Yucatán. 1997

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de noviembre de 2008)

Solución

Demostraremos en primer lugar este TEOREMA:

Los ángulos con lados perpendiculares son iguales.

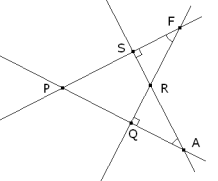
Sean los ángulos de vértices respectivos A y F y lados perpendiculares que se cortan respectivamente en P, Q, R, S (ver figura). En estas condiciones

Por ser ángulos opuestos por el vértice sabemos que

Por pertenecer al triángulo ARQ

Análogamente en el triángulo FRS

Introducimos los dos últimos resultados en la igualdad de los ángulos opuestos por el vértice y obtenemos

(c.q.d)

Si aplicamos el teorema anterior, de cuerdo a la perpendicularidad de lados que pide el enunciado, tenemos

que nos dice que los dos triángulos tienen los tres ángulos iguales y por lo tanto son semejantes.