Problema 486

Sean dos triángulos i tal que es perpendicular a , es perpendicular a , y es perpendicular a .

Demostrar que los triángulos y son semejantes.

Solución de Ricard Peiró:

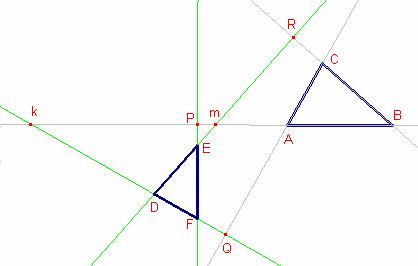
Supongamos que A y B son agudos.

Sea P la proyección del punto E sobre el lado .

Sea Q la proyección del punto F sobre el lado .

Sea R la proyección del punto D sobre el lado .

La recta DF corta la recta AB en el punto k.

La recta DE corta la recta AB en el punto m.

Los triángulos rectángulos , son semejantes, entonces, .

Entonces, .

Los triángulos rectángulos , son semejantes, entonces, .

Entonces,

Entonces, los triángulos y tienen dos ángulos iguales, entonces, son semejantes.

Con Cabri:

Figura barroso486.fig

Applet created on 1/11/08 by Ricard Peiró with CabriJava