Problema 487

Sea ABC un triángulo en el que ninguno de sus ángulos supera 120º. Sea G su Baricentro y F su punto de Fermat (punto interior al triángulo cuya suma de distancias a los vértices es mínima). Demostrar que se cumplen las siguientes relaciones entre la distancia FG entre el Baricentro y el punto de Fermat, siendo el área del triángulo:

(a) (b)

Vicario, V. (2008): Comunicación personal

Resolución: Utilizaremos la notación habitual en la geometría del triángulo. Sabemos según el contenido del problema 140 de esta revista que si G es el Baricentro de un triángulo y M es un punto de su plano, se cumple la siguiente relación fundamental siendo A, B, C los vértices del triángulo:

[1]

Identifiquemos el punto M por el punto de Fermat F del triángulo , que además de minimizar la suma de las distancias a los vértices, forma ángulos de 120º con los lados del mismo. Intentaremos determinar y a partir de la expresión [1] deduciremos el apartado (a) del problema.

Construyamos triángulos equiláteros cuyos lados sean los del triángulo de partida y exteriormente sobre cada lado del mismo. Es bien conocido que la suma que minimiza la suma de distancias a los vértices del triángulo coincide con cualesquiera de las tres distancias entre uno cualquiera de los vértices del triángulo y el vértice exterior del triángulo equilátero opuesto. Denotando por A´, B´, C´ los correspondientes vértices exteriores de los triángulos equiláteros opuestos a los vértices A, B, C, aplicando el teorema de los cosenos al triángulo BB´C y al ABC, y teniendo en cuenta la expresión , tenemos que

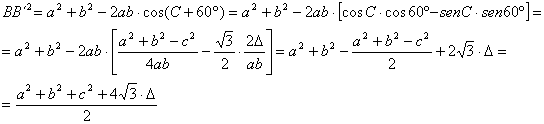
Así pues, tenemos que . [2]

Aplicando el teorema de los cosenos a los triángulos AFB, BFC y CFA tenemos las siguientes relaciones

o lo que es lo mismo

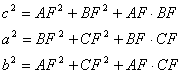[3]

y sumando miembro a miembro, tenemos que

[4]

Entonces se llega a la relación

o bien

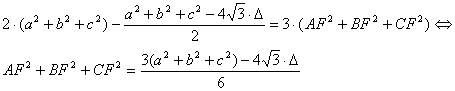
[5]

Teniendo en cuenta la expresiones clásicas para las longitudes de las medianas en un triángulo en función de las longitudes de sus lados (teorema de Apolonio) que se pueden obtener fácilmente a partir del teorema de Stewart

, ,

y teniendo en cuenta la conocida propiedad relativa a la longitud de los segmentos de las medianas desde el vértice al Baricentro tenemos que

[6]

Finalmente, llevando las expresiones [5] y [6] a la expresión [1] se obtiene

[7]

que demuestra el primer apartado.

El segundo apartado es una consecuencia inmediata del anterior y de la conocida desigualdad de Finsler-Hadwiger para un triángulo, (que es un refinamiento importante de la desigualdad de Weitzenböck) que afirma la desigualdad siguiente entre las longitudes de los lados de un triángulo y su área

Una demostración de esta desigualdad, por ejemplo, se puede ver en uno de los artículos publicados por el profesor F. J. García Capitán en el Extra 400 de esta revista. Aplicando esta desigualdad a la expresión [7] se obtiene inmediatamente la desigualdad