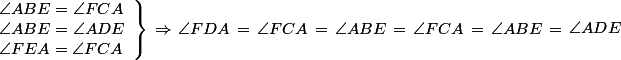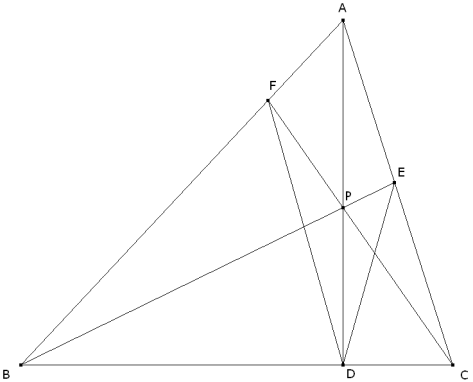
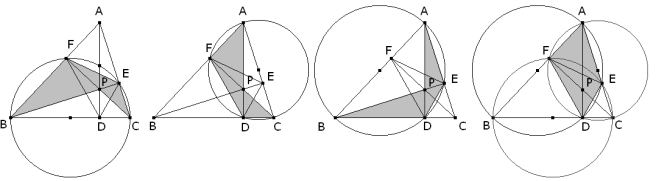
Problema 488. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Se escoge un punto arbitrario P en el interior de la altura AD de un triángulo ABC. Las rectas BP y CP cortan a los lados AC y AB en E y F, respectivamente. Demostrar que <PDF=<PDE. ¿Qué sucede si P está fuera del triángulo o la altura AD es exterior al triángulo?

Haruki (1980) Ontario Secondary School Mathematics Bulletin

[Ver problema 71 de trianguloscabri]

Sean G=PC y ED, y H =PB y FD ; y, construimos los puntos E´, F´ donde cortan BG, y CH, prolongadas a los lados AC y AB, respectivamente. Sean P´= CF´y BE´, P* = EF´y E´F.

Probar que : Los puntos P*, y P´ están sobre AD (¿es cierto para cualquier ceviana?).

Romero, J.B. (2008): Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de noviembre de 2008)

Solución

Hagamos la construcción del enunciado y estudiemos la figura.

figura 1

Desde un punto de vista proyectivo, podemos considerar dos haces de rectas, uno el de rectas BP y dos el de rectas CP. La biyección en la que

es una homografía. Es más, como P (intersección de cada recta por B con su imagen en las rectas por C) recorre una recta, sabemos que esa homografía es una proyección de haces de rectas.

La homografía de los haces de rectas anteriores nos lleva a que los puntos E y F sean homográficos en una homografía de la recta AB sobre la recta AC en la que

Esto último nos lleva a que la biyección del haz de rectas por D sobre sí mismo en la que

es también una homografía que podemos expresar analíticamente como

Tres posiciones particulares bastarán para determinar esta homografía.

Además si P coincide con el ortocentro del triángulo, DEF es el triángulo órtico de ABC (ver solución al problema 243).

figura 2

Por lo tanto, cunado P coincide con el ortocentro, las alturas del triángulo original son las bisectrices del triángulo órtico y se cumple

que nos lleva a que para todo punto P la homografía es

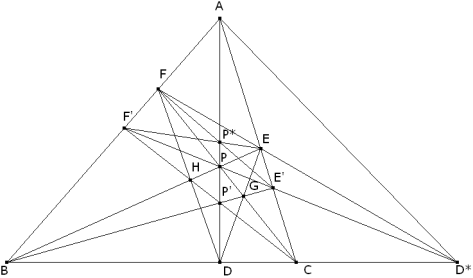
Sigamos ahora con la construcción del enunciado

figura 3

Como hemos dicho más arriba, las construcciones anteriores definen una homografía de la recta AB sobre la recta AC tal que

En esta homografía también se cumple que

y por las propiedades del cuadrilátero, las rectas BC y FE concurren en D*, conjugado armónico de D respecto B y C; lo que nos lleva a que esta homografía es una proyección de la recta AB sobre la recta AC con centro de proyección en D*.

En estas condiciones por las propiedades del cuadrilátero F’E’ pasará por D* y por lo tanto E’ es la imagen de F’ en la proyección anterior. Por las definiciones del enunciado, P, P’ y P*estarán alineados en el eje de homografía; pero en esta proyección el eje de homografía es AP=AD.

Como sólo hemos usado propiedades proyectivas, podemos concluir que la última parte del enunciado es cierto para cualquier ceviana.