Propuesto
por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de
Valladolid
Problema 488.- Se escoge un punto arbitrario P en el
interior de la altura AD de un triángulo ABC. Las rectas BP y CP cortan a los
lados AC y AB en E y F, respectivamente. Demostrar que <PDF=<PDE. ¿Qué
sucede si P está fuera del triángulo o la altura AD es exterior al triángulo?
Haruki
(1980)
[Ver
problema 71 de trianguloscabri]
Sean G=PC y ED, y H =PB y FD; y, construimos los puntos E´, F´ donde
cortan BG, y CH, prolongadas a los lados AC y AB, respectivamente.
Sean P´= CF´y BE´, P* = EF´y E´F.
Probar que:
Los puntos P*, y P´ están sobre AD (¿es
cierto para cualquier ceviana?).
Romero,
J.B. (2008): Comunicación personal
Solución.- a) A partir de las cevianas concurrentes en P, por aplicación de los teoremas de Menelao y Ceva se obtiene una cuaterna armónica: la formada por los puntos B, C, D y Q: (BCDQ) = -1. Para demostrar la igualdad de los ángulos bastará probar que la razón doble de las rectas DQ, DA, DE y DF es -1, pues eso significa que DQ y DA son bisectrices de FDE. Y esta razón doble, cortando estas rectas con EF y proyectando después desde A sobre BC es la razón (QDCB).
(DQ, DA, DE, DF) = (QREF) =(QDCB)=(BCDQ).
(Altura exterior y punto dentro de la altura.)
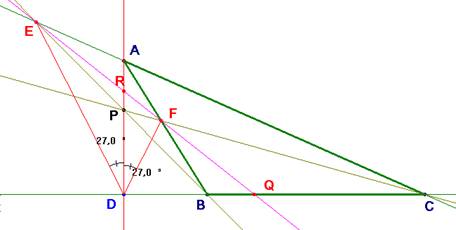
(Altura interior y punto también interior.)
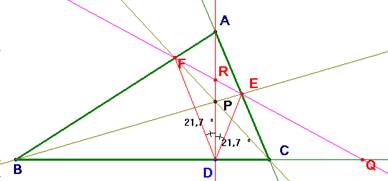
(Altura interior y punto fuera de ella.)
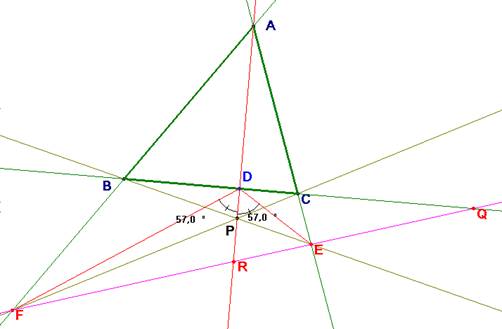
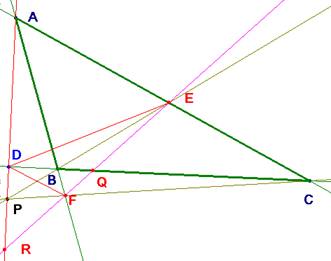Si P está fuera de la altura y ésta es exterior, se cambian los
papeles de algunos puntos. La situación es la anterior pero considerando como
triángulo el ACP con una altura sobre
AP y con cevianas concurrentes en B. Aquí los ángulos iguales son EDC y
CDF.
b) Sea Q el punto donde la recta EF encuentra al lado BC. Como ya hemos comentado la cuaterna (BCQD) es armónica, y también lo es (FEQR) (proyección desde A).
Considerando en el triángulo DEF las cevianas concurrentes en P, deducimos que los puntos H, G y Q están alineados y que (GHR’Q) es armónica.
En el triángulo HGD, como (GHR’Q) es armónica, deducimos que el punto P’ está sobre AD por la
unicidad del cuarto armónico.
Considerando ahora la proyección desde Q entre los lados AB y AC dada por (A,F,B)à(A,E,C). El eje de esta proyección es la recta que une A con FC·BE=P: la altura AD.
La imagen Y de F’ puede obtenerse así: se une F’ con C y B con Y. Estos puntos se han de cortar en el eje proyectivo, esto es, en P’, luego la imagen Y=E’.
En esa proyección también se corresponden F’ y E’. A partir de aquí, el punto P* por su definición está sobre el eje de esta proyección: la recta AD como queríamos demostrar.
El razonamiento sirve para cualquier ceviana, pues no se utiliza su condición de altura en ningún momento.
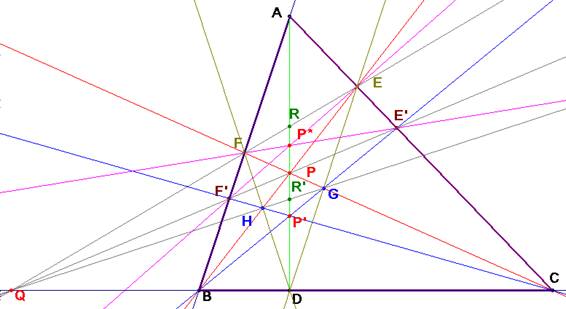
Finalmente probaremos que E’, F’, P y Q están alineados.
En el triángulo BF’C tomamos cevianas concurrentes en P (sin presuponer que P está alineado con E’, F’ y Q). Sea Q’ la proyección de P sobre BC desde F’. Como D=FH·BC resulta que (BCDQ’) es armónica y como el cuarto armónico es único Q=Q’ y por tanto E’, F’, P y Q están alineados.