Problema 489.- En un triángulo sea r el radio del círculo inscrito, R el radio del círculo circunscrito y H la altura mayor. Demostrar o refutar la siguiente desigualdad:

Polya, G. (1965). How to solve it. Editorial Trillas. México.

Propuesto por P. Erdös en The American Mathematical Monthly, vol 50 (1943) p. 124 y vol 51 (1944) p. 234-236.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

La proposición enunciada es, en general, falsa. Deduciremos un determinado contraejemplo que así lo demuestra.

Sea el segmento BC de longitud fija, que supondremos el lado desigual de la serie infinita de triángulos isósceles en los que el vértice A se desplaza a lo largo de la mediatriz de dicho segmento. A medida que el vértice A se aproxima al lado a del triángulo ABC, es decir, al segmento BC, se tiene obviamente que el ángulo se aproxima indefinidamente a 180º, las tres alturas en este tipo de triángulo tienden indefinidamente a 0, y el radio del círculo inscrito también tiende a 0. Entonces, aplicando el teorema de los senos generalizado, tenemos que

En consecuencia, queda claro que la desigualdad dada no se cumple en estos triángulos de esta posición límite.

---oooOooo---

Nota: Podemos demostrar de forma relativamente simple que la desigualdad anterior es cierta en todos los triángulos acutángulos. Es bien conocido que si ABC es un triángulo acutángulo arbitrario y H es su ortocentro, entonces se cumple la igualdad siguiente

Por otra parte, si suponemos, sin pérdida de generalidad, que , entonces se tiene que , y mediante un sencillo cálculo, utilizando relaciones entre ángulos de un triángulo y fórmulas trigonométricas elementales, se llega a la siguiente cadena de desigualdades:

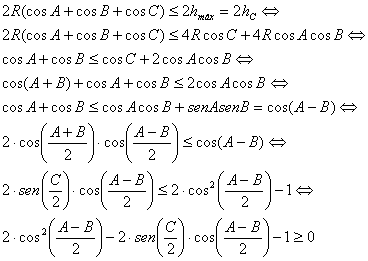
y la última desigualdad es obvia ya que el discriminante asociado a esta forma cuadrática es siempre positivo.

Para un triángulo rectángulo la desigualdad también se cumple ya que si A es el vértice del ángulo recto, (suponiendo sin pérdida de generalidad, que ) es conocido que los radios inscritos y circunscritos vienen dados por

con lo que se cumple la desigualdad

---oooOooo---