Problema 490

Los circuncentros de los cuatro triángulos que construyen cuatro rectas son concíclicos y los ortocentros están alineados

Dados un triángulo y una recta, ésta forma con cada par de lados de  aquél otros tres triángulos, entonces los cuatro circuncentros son 
concíclicosy los cuatro ortocentros están alineados. (aclaración del comité editorial)

Tomado de Internet, http://www.partnership.mmu.ac.uk/cme/Geometry/TriangleGeometry/MiquelCircles/GaussBod.htm

Solución del director

En primer lugar analicemos que las cuatro circunferencias circunscritas a ABC de ángulos a, b y c, ADE, a,d y e, FDB, f, d y 180-b y FEC, f, 180-e, c tienen un punto, P en común.

Las circunscritas a ABC y a ADE se cortan en A y en P.

Es : <APC=180-b, por lo que <CPE=<APE-<APC=(180-d)-(180-b)=b-d=(f+d)-d=f.

Por ello P está en la circunscrita a CFE también.

Tenemos <BPC=a, <CPF=180-e, luego <BPF=a+180-e=180-d, por lo que P pertenece también a la circunscrita a BFD, cqd.

Analicemos los circuncentros O1 O2 O3 y O4.

La recta O1 O2 es perpendicular a PA por ser una cuerda común a las circunscritas.

Igualmente O1O4 es perpendicular a PC. Luego < O2 O1 O4 y <APC o son iguales o suplementarios. En este caso se da la igualdad, < O2 O1 O4 = <APC=180-b.

De igual manera, la recta O3O4 es perpendicular a PF por ser cuerda común, y la recta O3O2 lo es a PD. <O4 O3 O2 =180-<FPD=180-<FBD=180-(180-b)=b.    

Al ser < O2 O1 O4  + <O4 O3 O2 =180-b + b=180, los circuncentros O1 O2 O3 y O4 son concíclicos, cqd .

Observemos ahora los ortocentros.

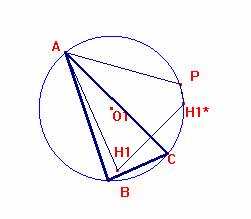
Sea el triángulo ABC cuyo ortocentro es H1, y su simétrico según AC es H1* que pertenece a la circunferencia circunscrita (ver por ejemplo el problema 166 de esta revista). El ángulo APH1* es:

<APH*1=<APC - <CPH1*=(180-b)- (<CAH1*)=180-b+(90-c)=90+(180-b-c)=90+a.

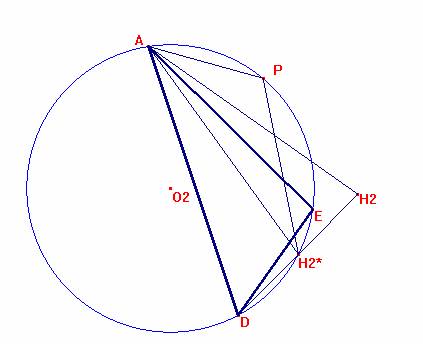
Consideremos ahora el ortocentro H2 de AED, y su simétrico H2* respecto a AE. El ángulo APH2* es:

APH2*=<APE - <EPH2* = (180-d)- <EAH2= 180-d-(e-90)=90-d-e=90+a.

Así, PH1*H2* están alineados , lo mismo que PH3* H4*.

Observemos la figura completa:

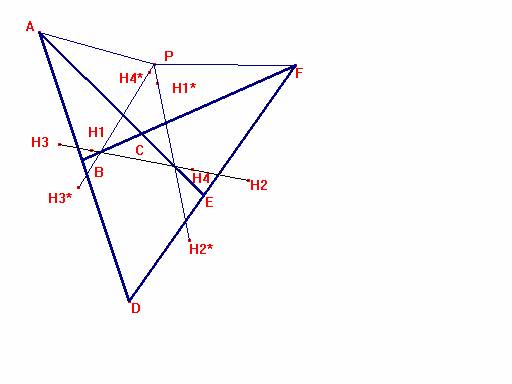
La recta AE es el eje de simetría de la rectas H1H2 y H1*H2*, luego es su bisectriz, y

la recta BF lo es de las rectas H3 H4 y H3*H4*.

Estudiemos el ángulo H1*PC. Es <H1*PF=<CPF-<H1*PF=(180-e)- (90+f)=180-e-f-90=c-90.

Estudiemos el ángulo H4*PC. Es <H4*PC=<CPA-<H4*PA=(180-b)- (90+a)=180-b-a-90=c-90.

Así pues, PC es bisectriz de H1*PH4*, y al estar C también en las bisectrices AE y BF, la distancia de C a las rectas H1* H2*, H1 H2 y H3* H4*, H3 H4 es la misma, lo que demuestra que los cuatro ortocentros están alineados.

Ricardo Barroso  Campos.

Didáctica de las Matemáticas

Universidad de Sevilla