Problema 490.- Los circuncentros de los cuatro triángulos que construyen cuatro rectas son concíclicos y los ortocentros están alineados.

Dados un triángulo y una recta, ésta forma con cada par de lados de  aquél otros tres triángulos, entonces los cuatro circuncentros son  concíclicos y los cuatro ortocentros están alineados (aclaración del comité editorial).

Tomado de Internet, http://www.partnership.mmu.ac.uk/cme/Geometry/TriangleGeometry/MiquelCircles/GaussBod.html

Solución.-

With any three points X,Y,Z on the sides of triangle ABC, the circles AYZ, BZX, CXY meet in a point.

The circles are called the Miquel circles for the triple X,Y,Z, and the point common to them is called the Miquel point.

P1.- De la referencia en Internet dada en el enunciado tomamos la definición del punto de Miquel. Si M está en las circunferencias que pasan por B y C, el ángulo <XMZ = 180 –B y < XMY =180 – C por tanto < ZMY =180 – A, que prueba que también está M en la circunferencia que pasa por A.

P2.- Otra propiedad que vamos a usar, obtenida también desde la referencia de Internet es que los centros de un conjunto de circunferencias de Miquel de un triángulo forman un triángulo semejante al inicial, de demostración sumamente sencilla:

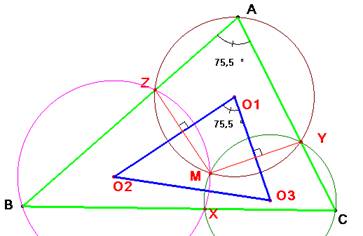
El eje radical es perpendicular a la recta de los centros, por eso el ángulo en O₁ es suplementario del ángulo ZMY y por tanto, igual al ángulo <A.

P3.- Centrándonos en el problema, lo primero que vamos a probar es que las cuatro circunferencias circunscritas se cortan en un punto común M.

Considero el triángulo T₃ = A₁₂A₁₄A₂₄ y la transversal r₃ = A₃₄A₁₃. El punto de Miquel correspondiente a esta situación es el de intersección de las circunferencias K₁ = A₂₄A₃₄A₂₃ con K₄ = A₁₂A₂₃A₁₃ y con K₂ = A₁₄A₁₃A₃₄. Para el triángulo T₂ = A₃₄A₁₃A₁₄ y la transversal r₂ = A₁₂A₂₄ el punto de Miquel es el común a las circunferencias K₁, K₄ y K₃=A₁₄A₁₂A₂₄. Por tanto M yace sobre las 4 circunferencias K_i.

P4.- Los circuncentros yacen en una misma circunferencia.

Según la propiedad P2 para el triángulo T₃, el ángulo formado en el vértice A₂₄ es igual al formado en el vértice O₁ del triángulo O₁O₂O₄, esto es, < A₁₂A₂₄A₁₄= < O₂O₁O₄. La misma propiedad en el triángulo T₁ nos da ahora que el ángulo en A₂₄ es igual al del vértice O₃ del triángulo O₃O₂O₄. Por ello los ángulos <O₂O₁O₄ y <O₂O₃O₄ son suplementarios y el cuadrilátero de los circuncentros es inscriptible.

P5.- Los ortocentros están alineados.

Ya sabemos que M, el punto de Miquel, pertenece a las cuatro circunferencias circunscritas. Suponiendo que pertenece a K₃, utilizando el problema nº 192 publicado en esta revista, sabemos que sus simétricos S₄, S₁, y S₂, respecto de los lados del triángulo T₃ = A₁₂A₂₄ A₁₄ están alineados y además la recta que definen contiene al ortocentro H₃ de este triángulo.

Si ahora utilizamos M como punto de la circunferencia K₄, concluimos que también están alineados sus simétricos respecto de los lados del triángulo T₄ = A₁₂A₂₃A₁₃. Esa recta contiene también el ortocentro H₄. Y como dos de estos simétricos coinciden con dos de los anteriores tenemos que los simétricos de M respecto de los 4 triángulos, así como los respectivos ortocentros se encuentran todos sobre una misma recta, como pretendíamos demostrar.