Problema 2.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva).

Probar o refutar si en todo triángulo ABC, al menos uno de los radios de las circunferencias exinscritas es mayor o igual que una de sus bisectrices interiores .

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Utilizaremos la notación habitual en la geometría del triángulo. En realidad probaremos más de lo que se pide. Demostraremos que se cumplen las siguientes desigualdades

de las que se deduce fácilmente el resultado razonando por reducción al absurdo. En efecto, si los tres radios exinscritos fuesen menores, en algún orden, a las tres bisectrices interiores, tendríamos claramente una contradicción con las desigualdades anteriores. Demostraremos 4 lemas que nos son necesarios.

Lema 1: “En todo triángulo ABC se cumple: ”.

Demostración: Basta con utilizar la fórmula de Herón y la expresión . ·

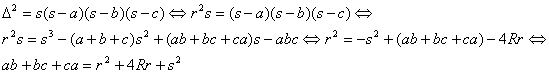Lema 2: “En todo triángulo ABC se cumple la desigualdad: ”.

Demostración: Utilizaremos las expresiones bien conocidas para las longitudes de las bisectrices interiores de un triángulo:

, ,

Por otra parte, es fácil observar que se tiene

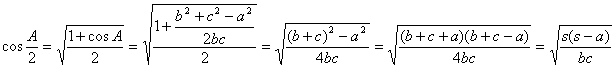con lo que entonces ..

Utilizando la desigualdad de Cauchy-Schwarz, y la desigualdad elemental , tenemos que

·

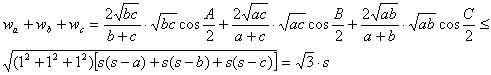Lema 3: “En todo triángulo ABC se tiene que ”.

Demostración: Basta observar la siguiente cadena de igualdades

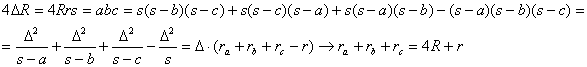
puesto que ·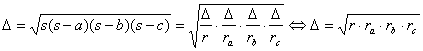

Lema 4: “ En todo triángulo ABC se cumple la desigualdad: ”.

Demostración: Utilizaremos la conocida desigualdad de Jensen, junto con el hecho de la convexidad de la función en el intervalo . Aplicando dicha desigualdad tenemos que

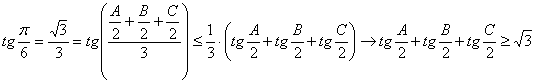
Además, empleando el lema 1, tenemos claramente entonces que

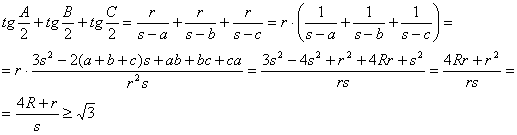
donde la desigualdad se ha obtenido a partir de la desigualdad de Jensen. ·

Finalmente, utilizando el lema 3 y la reducción al absurdo comentada al inicio de la resolución de este problema, concluye la demostración.