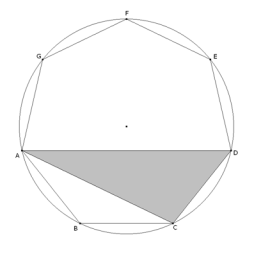
Problema 493. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Hallar el área del único triangulo escaleno (modulo rotaciones) formado desde los tres vértices de un heptágono regular, teniendo los ángulos pi/7, 2pi/7, y 4pi/7, respectivamente, inscrito en una circunferencia de radio R.

Matemática Elemental, Tomo I, N.2, Enero,1932, en p.28

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de noviembre de 2008)

Solución

Se encuentra la solución de este enunciado en el problema 34-2 de la página 257 de:

Norte de problemas,

Rey Pastor y Gallego Díaz,

Editorial Dossat

Si examinamos la siguiente figura podemos deducir que se trata de calcular el área del triángulo gris de la figura, cuyos lados son:

CD, lado del heptágono regular;

AC, lado de un heptágono estrellado de segunda especie;

AD, lado del heptágono estrellado de tercera especie.

Se verifica:

.

Pero:

.

Para calcular el producto de los senos consideramos la ecuación:

.

Dividiendo por Z-1 obtenemos:

que es una ecuación recíproca.

Dividiendo ahora por Z³ y agrupando convenientemente los términos (ecuación recíproca):

.

Pero

Las soluciones en Z de esta ecuación son las de la ecuación Z³ - 1 = 0 , es decir

cuyos recíprocos son

Los valores de son:

.

Llamando a , 2x, la anterior ecuación se escribe:

.

Y, en virtud de que las raíces de esta ecuación son

podemos escribir la identidad

y dando a x el valor 1:

.

Los paréntesis valen, respectivamente

.

Por lo tanto:

o sea:

y sustituyendo en la expresión del área del triángulo, obtenemos finalmente:

.