Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 493 .- Hallar el área del único triangulo escaleno (módulo rotaciones) formado desde los tres vértices de un heptágono regular, teniendo los ángulos p/7, 2p/7, y 4p/7, respectivamente, inscrito en una circunferencia de radio R.

Matemática Elemental, Tomo I, N.2, Enero, 1932, en p.28.

Solución

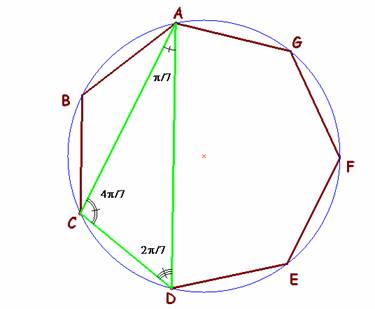
En función del radio de la circunferencia inscrita los lados de este triángulo miden 2Rsen, 2Rsen y 2Rsenrespectivamente. El área del mismo es igual al semiproducto de dos lados por el seno del ángulo comprendido, se obtiene [ACD] =2R2 · sen·sen·sen.

Ahora vamos a expresar en función del radio ese producto de senos. Teniendo en cuenta que son ángulos de un triángulo tenemos:

sen·sen·sen= sen·sen·sen=.

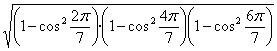El radicando de esa expresión lo vamos a calcular como el valor para x = 1 de un polinomio cuyas raíces son los cuadrados de esos cosenos.

Las soluciones complejas de la ecuación z7 = 1 tienen como parte real los números cos, cos y cos· Separando la solución real z = 1, la ecuación resultante es la ciclotómica de grado 6, esto es,                  

z6+ z5 +  z4 + z3 + z2 + z + 1 = 0.

Esta ecuación admite el cambio y = z + z –1 por tratarse de una ecuación recíproca (contiene las inversas de las raíces). En el caso de la ecuación ciclotómica, la nueva variable es el doble de la parte real de las raíces séptimas de la unidad, que es el doble del coseno. Tomando en vez de éste el cambio y = , la ecuación transformada (de tercer grado) tiene por raíces los cosenos del problema.

Si, a su vez, hallamos a partir de esta la ecuación cuyas raíces son sus cuadrados, habremos llegado al final de nuestro recorrido encontrando el polinomio que para  x = 1 da con el valor buscado.

A partir de

z6 + z5 +  z4 + z3 + z2 + z + 1 = 0.     (E1)

dividimos la ecuación por z3, y agrupamos los términos como sigue:

(z3 + z-3) +(z2 + z-2) +(z + z-1) +1 = 0.    (E2)

Realizamos en E2 el cambio dado por

y =       (C1)

Para ello vamos a calcular por separado cada paréntesis de (E2).

(z + z-1) = 2y;                                    z + z-1 = 2y

(z + z-1)2 = z2 + z-2 +2;                       z2 + z-2 = 4y2 –  2

(z + z-1)3 = z3 + z-3 +3(z + z-1);          z3 + z-3 = 8y3 – 6y

Sustituyendo todo en E2 resulta

8y3 + 4y2 – 4y –  1= 0   (E3)

Esta es la ecuación cuyas soluciones son los cosenos. Para obtener la que tiene como raíces los cuadrados se cambia y por –y, se multiplican los dos polinomios y en el resultante se hace finalmente el cambio de x = y2.

Resulta

(8y3 + 4y2 – 4y –  1)·( –8y3 + 4y2 + 4y –  1) = –64y6 + 80y4 – 24y2 + 1

Finalmente

– 64x3+ 80x2 – 24x + 1 = 0   (E4)

llegamos a la ecuación cuyas soluciones son los cuadrados de los cosenos.

Si   p(x) = – 64x3+ 80x2 – 24x + 1,

=  ·p(1) = =, de aquí concluimos que el área del triángulo que buscamos es

[ACD] =2R2 · sen·sen·sen= R2.